Stress from Bending
Quick Start
Suppose you have a thin coating and want to know how much stress it contains. Coat it onto a thin strip of metal and measure the distance moved, D over length L. The stress is easily calculated with a few more parameters.
Stress from Bending
Sometimes you need to know how much stress there is within a coating, and how it changes with time, cure rate, composition etc.
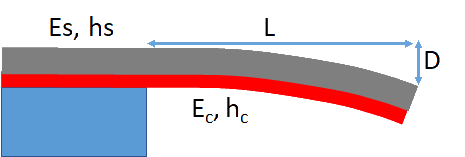
The procedure is simple in principle. Knowing the coating's thickness hc, on a strip of material thickness hs and moduulus Es, you measure the deflection D over a length L using some sort of laser system. The usual equation (sometimes attributed to Stoney, sometimes to Corcoran) calculates the stress σ from the first part of the equation which ignores the modulus Ec of the coating. If you have some idea of this modulus Ec (e.g. by measuring its bending in a very similar manner) then you can enter this value so the extra term kicks in, though it usually makes little difference:
`σ=(DE_sh_s^3)/(2h_cL^2(h_s+h_c)) + (DE_c(h_s+h_c))/(0.66L^2)`
The 2 and the 0.66 on the bottom of each equation are the result of assuming that the Poisson term (1-ν)=2/3. There are plenty of papers with plenty of refinements and subtleties. But we generally only need to know relative stresses and as long as hc and Ec don't vary wildly between samples, you just need to know that σ is proportional to D!
Typical moduli of support materials are Steel=200GPa, Brass=100GPa, Silicon=160GPa, Al=70GPa


