Coffee Fermentation

//One universal basic required here to get things going once loaded
window.onload = function () {
    //restoreDefaultValues(); //Un-comment this if you want to start with defaults
    Main();
};
//Any global variables go here


//Main is hard wired as THE place to start calculating when input changes
//It does no calculations itself, it merely sets them up, sends off variables, gets results and, if necessary, plots them.
function Main() {
    saveSettings();

    //Send all the inputs as a structured object
    //If you need to convert to, say, SI units, do it here!
    const inputs = {
        mgpg: sliders.Slidemgpg.value,
        V: sliders.SlideV.value,
        L: sliders.SlideL.value/100, //% to fraction
        B: sliders.SlideB.value,
        K1: sliders.SlideK1.value,
        K2: sliders.SlideK2.value,
        P: sliders.SlideP.value,
        kd: sliders.Slidekd.value,
        G: sliders.SlideG.value,
     }

    //Get all the resonses as a structure
    const result = CalcIt(inputs)

    //Set all the text box outputs
 //   document.getElementById('TgWet').value = result.TgWet
    if (result.plots) {
        for (let i = 0; i < result.plots.length; i++) {
            plotIt(result.plots[i], result.canvas[i]);
        }
    }

}

//Here's the real app calculation
function CalcIt({mgpg, V, L, B, K1, K2, P, kd, G}) {
    //The structure automatically has the names provided from input
    //By convention the values are provided with the correct units within CalcIt
    let BPts=[], OPts=[], C=0
    // const tstep=1
    // for (let t = 0; t <= 48; t+=tstep) {
    //     C=mgpg*L*(1+(V+1)*B/mgpg-Math.exp(-(K1*Math.exp(P*t)+K2)*(t*(V+1))))/(V+1)*(Math.exp(-kd*t))
    //       BPts.push({x:t,y:C})
    // }
    const tstep=0.1
    const cInc=G/V*tstep
    let cOut=mgpg/V, cIn=B, Diff=0, K1P=K1, Lost=0
    for (let t = 0; t <= 48; t+=tstep) {
        OPts.push({x:t,y:cOut*V})
        BPts.push({x:t,y:cIn})
        K1P=K1*Math.exp(P*t)
        Diff=(L*cOut-cIn)*tstep*(K1P+K2)
        cOut += (cInc - Diff)
        Lost = kd*tstep*cIn
        cIn += (Diff - Lost)
    }

    //Now we return everything - text boxes, plot and the name of the canvas, which is 'canvas' for a single plot
    const prmap = {
        plotData: [BPts,OPts], //An array of 1 or more datasets
        lineLabels: ["C in bean","C in ferment"], //An array of labels for each dataset
        hideLegend: false,
        xLabel: 't&hr', //Label for the x axis, with an & to separate the units
        yLabel: 'Ct&mg/g', //Label for the y axis, with an & to separate the units
        y2Label: null, //Label for the y2 axis, null if not needed
        yAxisL1R2: [], //Array to say which axis each dataset goes on. Blank=Left=1
        logX: false, //Is the x-axis in log form?
        xTicks: undefined, //We can define a tick function if we're being fancy
        logY: false, //Is the y-axis in log form?
        yTicks: undefined, //We can define a tick function if we're being fancy
        legendPosition: 'top', //Where we want the legend - top, bottom, left, right
        xMinMax: [,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
        yMinMax: [,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
        y2MinMax: [,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
        xSigFigs: 'P3', //These are the sig figs for the Tooltip readout. A wide choice!
        ySigFigs: 'P3', //F for Fixed, P for Precision, E for exponential

    }
    return {
        plots: [prmap],
        canvas: ['canvas'],
    };
}
            

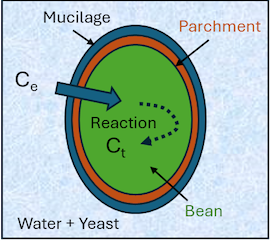How the published model works

We have a starting external concentration, C₀ in mg/g of water of some molecule of interest such as phenylethanol and we want to know the concentration at time t, C_t, inside the bean.

It depends, first, on V, the relative volume of coffee beans to water, `V=V_c/V_w`. If V=1 and if there is no destruction of the molecules inside the bean, the equilibrium value is 50% of the original. For higher values such as the default 1.4, it's lower. Next there is a % of free molecules in the water, L, typically 100% but sometimes adding, say, yeast, can reduce this to 40%.

For those molecules that exist already in the bean we need a starting value B mg/g.

We then have potentially two diffusion coefficients. If we have parchment, then the K₁ value is mixed with a time-dependent parchment value, p, which can describe how the parchment gets more resistant (more negative p) over time. If there's no parchment (or if the parchment isn't a barrier to the molecules) then you just use K₁ with p = 0 and K₂ is set to 0.

Once in the bean, the molecules might be actively destroyed (metabolised) by one or more (enzymic) reactions. Here we assume two reactions with rates k_d1 and k_d2. The fraction of reaction 1 is g and of reaction 2 is (1-g).

The whole model is called MTER-DFORP, Mass Transfer with Evolving Resistance - Double First Order Reaction in Parallel. You can make it simple MT by setting K₂, P, k_d1 and k_d2 to zero to understand the basics, then add more complexities as needed. Here's the equation:

`C_t=C_0L(1 + ((V+1)B)/C_0-e^(-(K_1e^(pt)+K_2)t(V+1))/(V+1))("g"e^(-k_(d1)t)+(1-g)e^(-k_(d2)t))`

However, for the purposes of the app the benefits of the DFORP are small and it was easy to get confused, so for the app the k_d2 term has been removed, along with g, so it's an MTER-FORP equation with a single k_d parameter:

`C_t=C_0L(1 + ((V+1)B)/C_0-e^(-(K_1e^(pt)+K_2)t(V+1))/(V+1))(e^(-k_(d)t))`

To replicate the plots in the paper (though they are in %T we are in mg/g), set V = 1.4, L = 1 and S = 0, then use the following values. Values not specified are all 0. See below for the additional G parameter:

• Phenylethanol, no parchment: K₁ = 0.041.
• Phenylethanol, with parchment: K₁ = 0.031, K₂ = 0.008, P = -0.056, with k_d = 0.
• Isoamyl acetate, all cases: K₁ = 0.003, k_d = 0.052, .
• For Butanal: K₁ = 0.008, k_d = 0.14

Finally, if you add a lot of yeast then Butanal is strongly absorbed and L reduces to 0.4.

An earlier paper² from the Hadj Salem group provided data on Lactic Acid, Alanine, Glutamic Acid and Fructose. Their data included amounts originally in the beans (0 mg/g for lactic acid, 0.3 for alanine, 0.9 for glutamic acid and 8 for fructose. In each case we have parameters for parchment-free and with parchment and both V and L = 1. Unspecified parameters are all 0. The results with parchment are identical with/without mucilage or fermentation:

• Lactic Acid, no parchment: K₁ = 0.036
• Lactic Acid, with parchment: K₁ = 0.005
• Alanine, no parchment: B = 0.3, K₁ = 0.044
• Alanine, with parchment: B = 0.3 K₁ = 0.018, p = -0.035
• Glutamic Acid, no parchment: B = 0.9, K₁ = 0.042, k_d = 0.009
• Glutamic Acid, with parchment: B = 0.9, K₁ = 0.017, K₂ = 0.002, p=-0.01
• Fructose, all cases: B = 8, k_d = 0.024

How this model works

Any algebraic model can be replaced by a numerical version. In order to add an extra feature, the possibility of increase of external concentration via fermentation, it was simple to convert the original to a numerical equivalent, test that the results were the same (which they were), then to add the Growth rate, G. In this version, G is a constant but with extra parameters we can make it whatever is required.