Modulus Conversions

//One universal basic required here to get things going once loaded
window.onload = function () {
    //restoreDefaultValues(); //Un-comment this if you want to start with defaults
    Main();
};

//Main() is hard wired as THE place to start calculating when inputs change
//It does no calculations itself, it merely sets them up, sends off variables, gets results and, if necessary, plots them.
function Main() {
    //Save settings every time you calculate, so they're always ready on a reload
    saveSettings();

    //Send all the inputs as a structured object
    //If you need to convert to, say, SI units, do it here!
    const inputs = {
        E: sliders.SlideE.value,
        G: sliders.SlideG.value,
        K: sliders.SlideK.value,
        nu: sliders.Slidenu.value,
    };

    //Send inputs off to CalcIt where the names are instantly available
    //Get all the resonses as an object, result

    const result = CalcIt(inputs);

    //Set all the text box outputs
    document.getElementById('FromE').value = result.FromE;
    document.getElementById('FromG').value = result.FromG;
    document.getElementById('FromK').value = result.FromK;


    //You might have some other stuff to do here, but for most apps that's it for Main!
}

//Here's the app calculation
//The inputs are just the names provided - their order in the curly brackets is unimportant!
//By convention the input values are provided with the correct units within Main
function CalcIt({ E,G,K,nu}) {
    // 
`G=E/(2(1+ν)) and K=E/(3(1-2ν))`
    // 
`E=2G(1+ν)) and K=(2G(1+ν))/(3(1-2ν))`
    // 
`E=3K(1-2ν) and G=(3K(1-2ν))/(2(1+ν))`
    const GfromE=E/(2*(1+nu)), KfromE=E/(3*(1-2*nu))
    const EfromG=2*G*(1+nu),KfromG=2*G*(1+nu)/(3*(1-2*nu))
    const EfromK=3*K*(1-2*nu),GfromK=3*K*(1-2*nu)/(2*(1+nu))
 
    return {
        FromE: "G : "+ GfromE.toFixed((2)) + ", K : "+ KfromE.toFixed((2)),
        FromG: "E : "+ EfromG.toFixed((2)) + ", K : "+ KfromG.toFixed((2)),
        FromK: "E : "+ EfromK.toFixed((2)) + ", G : "+ GfromK.toFixed((2)),

    };
}

            

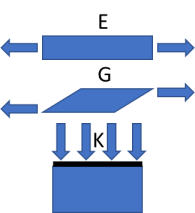Any modulus is simply stress/strain, the ratio between the force applied and the relative change in dimensions. The normal tensile test, from pulling the sample, gives E, also called the Young's modulus.

If you measure the deformation from shear (e.g. in a rheometer) you calculate the shear modulus G.

And if you compress the sample, you measure the bulk (or compression) modulus, K

They are inter-related via the Poisson ratio, ν by:

(From E) `G=E/(2(1+ν)) and K=E/(3(1-2ν))`

(From G) `E=2G(1+ν) and K=(2G(1+ν))/(3(1-2ν))`

(From K) `E=3K(1-2ν) and G=(3K(1-2ν))/(2(1+ν))`

The most dramatic implication of these equations takes a relatively dull rubber with E=50MPa and attempts to use it to even out pressures in, say, a printing press. Because the rubber is being squashed, and because a rubber might have ν=0.499, the relevant modulus is the bulk modulus K= 50/(3(1-0.998))=8.3GPa, i.e. not rubbery at all. So rubber is not good at compensating for uneven contacts. Sooner or later, everyone works out that if you need such compensation then you must use a foam, not a rubber.

The Poisson Ratio

When you pull an object in, say, the X-plane, a fraction of that pull will appear as a shrinkage in, say, the Y-plane. That fraction is the Poisson Ratio ν. If you don't know a value you can get a good approximation by deciding if it's "foamy" (ν=0.1), "normal" (ν=0.3) or "rubbery" (ν=0.499). If you have an exotic material it might be "auxetic" which is ν less than 0, i.e. if you pull it in one direction it expands in another.

Limitations

The theory here is used widely for many materials, but there are plenty of exceptions. As pointed out by web-handling expert Dr David Roisum a good example of where the simple theory does not apply is paper. The classic quoted range of 0-0.5 for Poisson ratio again is not valid for such fibrous materials. I once read that the Poisson ratio in the Z-direction could be large (>1) and negative. But then elsewhere I read that it's small and positive. It took me a while to work out what was going on. Although ν_XZ = ν_ZX for normal bulk materials (indeed, as a default, we just give a single value ν), this is not the case for paper. There is a large Z-direction change if you pull in the X plane, but there's almost no change in the X plane if you push in the Z plane.