Polymer swelling
Quick Start
Polymer swelling can be analysed by the Flory-Rehner equation which shows how the swelling is related to the MWt of chains between crosslinks - with larger values allowing more swelling. The swelling is shown as a ratio of volumes which is identical to 1/φ2 which is the concentration of polymer in the swollen gel.
Check your intuitions about the effect of the measure of "happiness" (the Flory-Huggins χ where 0.5 is starting to be unhappy) and the sizes of the polymer and solvent. The density of the polymer, ρ2 play a minor role.
Flory-Rehner
When a solvent is added to a crosslinked polymer, the polymer will swell. The amount of swelling depends on two factors:
- How soluble the (uncrosslinked) polymer is in the solvent - and as we have seen in the Polymer Solubility app, that's controlled by Flory-Huggins and the χ parameter;
- The length (or, in this theory, the MWt) of the chains between crosslinks. Obviously the shorter the length (the higher the crosslink density), the less the swelling.
These effects are captured in the Flory-Rehner equation. Where φ2 is the volume fraction of polymer in the swollen state, V1 is the molar volume of solvent, ρ2 is the density of the polymer, M2 is the polymer MWt and Mc is the MWt of chains between crosslinks:
`-[ln(1-φ_2) + φ_2 + χφ_2²] = ρ_2V_1/M_c(1-2M_c/M_2)(φ_2^0.333-φ_2/2)`
It's a somewhat awkward equation and what we plot depends on what we want to see.
The left-hand graph plots Mc versus the observed swelling ratio (Vswollen/Voriginal = 1/φ2) so you can see how different crosslink densities will behave, as discussed below. If you have the experimental value for the swelling ratio and you know the other parameters, you can read Mc off the graph using the mouse.
To understand the graph, let's look at the value of Mc when the x-axis value is 10. This means that the volume of swollen polymer over unswollen is 10 so the amount of polymer, φ2 is small (10%) because it's 90% solvent. The value of Mc must be rather high to allow so much swelling. Now look at where the x-axis starts at 1, i.e. when there is zero swelling because there is 100% polymer, i.e. φ2=1, so if you have a very small swelling ratio (1/φ2 is small) that means either that the polymer is incompatible with the polymer or that Mc is very small, i.e. there are very short chains between crosslinks, so the crosslink density is high.
As χ gets large the calculations start to become meaningless and the graph stops at the point where the formula breaks down.
The right-hand graph plots the swelling ratio against the crosslink density - obviously the higher the density, the smaller the swelling, with the value asymptoting to 1, i.e. zero swelling.
Cross-link density
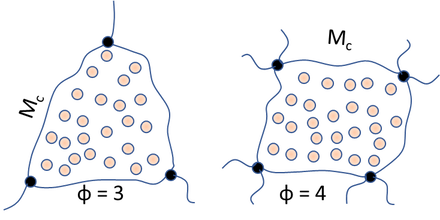We can also plot swelling versus the cross-link density, v, using the average functionality of a cross-link point, φ, via:
`v=(2ρ_2)/(φM_c)`
The units are usually mol/cc but for plotting it was nicer to have mol/l.
