Probe Tack Test

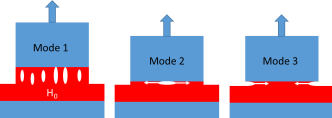The probe tack test is a very indirect way of looking at PSAs. But read below for an update on this! Although many of the things it measures are common to the other measures such as shear and the all-important peel, it's really just a butt joint test which is wildly different in physics from shear and peel. So it's impossible to formulate a PSA directly via the probe tack test which pulls up vertically and can fail in 3 modes, with Mode 1 being discussed here.

The test has a distinctive rapid rise in measured stress, σ versus strain ε as the probe is pulled upwards, then as cavitation bubbles of diameter d₀ start to appear, the stress drops off. At a strain of ε_max there is separation. We're interested in knowing the maximum stress σ_max and the work of adhesion W_A.

The measured values depend on the initial thickness of the adhesive, H₀, the velocity of pull, V, then some material properties μ₀ which is the low frequency shear modulus, G₀ which is the "interfacial threshold energy", whatever that means, and a characteristic pull-off speed v*. Finally there's a power-dependence α which is typically around 0.5 and so our actual pull-off speed is referenced against it.

As is well known, increasing the crosslink density changes the beahviour significantly. The paper uses a somewhat sophisticated formula for which it is hard to judge the parameters, so the app uses a 0-10 scale of crosslinks, where the effective μ₀ and v* are increased proportionately. As the authors freely admit, their crosslink calculations are not precise, so this simplification in the app is not too far from the spirit of the paper.

The basic equation relates the stress σ to the strain ε and the size of the cavitation bubble d via:

`σ=εH_0(H_0/d)^3`

So we need to know d as a function of ε. The equation, which needs to be solved numerically is:

`(δd)/(δε)=H_0((v"*")/V)((μ_0H_0)/G_0(ε^2H_0^5)/d^5-1)^(1/α)`

However, before the maximum stress σ_max the formula has a constant value of d₀, which creates the linear ramp at the start. σ_max is reached at ε_max given by:

`ε^(max)=sqrt(G_0/(μ_0H_0)(d_0/H_0)^5)`

Finally we need to estimate the work of adhesion, W_A via:

`W_A=G_0(V/(v"*"))^((2α)/(α+2))((μ_0H_0)/G_0)^(α/(α+2)`

You will notice that the equations have no constants. These are all "scale" approximations so constants are unnecessary. All we are trying to do is get a feel for what happens when we change key variables. As the paper shows, the fits to experimental data are generally good, though they cannot find a value of α that gives a good fit to the stress, strain and work of adhesion simultaneoulsy. As mentioned at the start, the authors are open about the limitations of this simple approach and list a set of possible refinements for more sophisticated models. Let's just be grateful that after decades of handwaving about the probe tack test we have a plausible and insightful model with which to explore.

G₀, v*, μ₀

G₀ is the "interfacial threshold energy" or "intrinsic adhesion energy" or "threshold toughness" which is typically 20x larger than the work of adhesion (surface energy) W. A typical fracture mechanics definition of G₀ is

`G_0=W+kTNΣ`

where N is a number of repeat units in a polymer and Σ is a density of interfacial chains. However, those definitions apply when we have chains going across and interface, so it's hard to relate them to a PSA. Equating G₀ to W is underestimating its value. I've given it a default of 0.5, i.e. a factor of ~10 higher than W. In principle you can measure it from the peel energy extrapolated to zero velocity, but most of us find this to be a tricky process.

Similarly, v* is classically given by

`v"*"=E/(2Σζ_0Ν)`

where ζ₀ is a monomer friction coefficient. In the paper, v* is defined as:

`v"*"=(μ_0G_0ω_c)/σ_c^2`

but then we need to know ω_c the glass transition frequency and σ_c which is the stress at separation at the interface. An alternative is l_c.ω_c, where l_c is (1/c)^1/3 where c is the crosslink density. Most of us have no idea of any of these parameters, but we get the general idea: things tend to get more rigid at higher peel speeds, but the effect of speed depends on the initial rigidity, with low v* being more rigid.

Finally μ₀ is the low frequency G' value. For a typical PSA, G' at 1Hz is 0.1MPa, i.e. 100kPa as this is the Dahlquist criterion. If you look at the Ideal PSA app you will see that "low" means 0.001Hz or less, so a good estimate for μ₀ is a factor of 100 lower, i.e. 1kPa.

A Direct Link from Probe test to Peel

It has always been regretted that there has never been a direct link between probe tack data and the peel test data we generally require. All that changed in 2020 when Creton, Ciccotti and coworkers published² a direct experimental/theoretical connection between them. Admittedly, the link requires a very special peel test rig and some fancy adjustments of time-scales (WLF-style), but at least we have a link. No doubt this paper will generate a lot of interest and, hopefully, a new standard approach to PSA science. If things become appable, I will appify them.

Acknowledgement

Prof Yamaguchi kindly confirmed that the app is working adequately (though any errors remaining are my fault) and provided some helpful insights into the tricky G₀, v* and μ₀ values, but again, any errors in their descriptions are mine.