Dahlquist Criterion

When a PSA is (lightly) pressed against a surface the adhesion would be maximised if it could flow round all the peaks and troughs in the surface to make full, perfect contact. This is not because rough surfaces increase adhesion because of a mythical higher surface area. The extra surface area of a typical "rough" surface is probably <5% higher than the equivalent planar surface. In fact the opposite is true: rough surfaces are a severe problem for PSA. If the (light) pressure gives contact with only the peaks of the surface then adhesion is reduced catastrophically. Here is a rough surface¹ where R is the Radius of the typical bumpy feature on the surface and h is the height of that bump above the mean level of the surface which is shown as a horizontal dotted line.

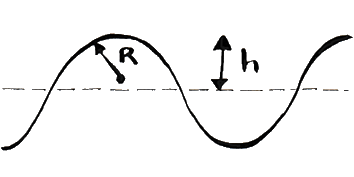
If the pure Work of Adhesion between the surface and the adhesive (not to be confused with the real adhesive strength of a PSA) is W (typically 40-50 mN/m), then the ability of a material to flow into this surface is defined via a critical modulus, G_c given by:

`G_c=W.sqrt(R/h^3)`

An alternative formula from Prof Michele Ciavarella is described below.

When the adhesive's modulus G < G_c the adhesive will spontaneously flow (even with the lightest of pressures) into the peaks and troughs and maximum adhesion will be attained. Those who know about JKR experiments in Practical Adhesion will see the analogy with radii, distances, moduli and the attractive power of W.

What this means is that you need a very low modulus, G, for sharp features (R is small) and/or deep features (h is large). Although a high W can help, in practice for most materials W varies over a small range of ~25 to 60 mN/m whereas R can vary by factors of 100.

With the default parameters of 50mN/m, R=5μm and h=1μm, a very typical surface for a PSA, G_c is ~0.1MPa. In 1969 Carl Dahlquist, who worked for 3M came up with a statement that became a "Criterion" bearing his name:

"For measurable quick tack, the elastic modulus must be below a certain fixed value which is fairly independent of the nature of the adhesive, the adherend and the applied pressure."

He decided that the "certain fixed value" should be 0.3MPa, which makes sense in terms of the default calculation. Of course, this is only a rule-of-thumb; for any specific application with known W, R and h you can create your own criterion. But 0.3MPa has been a useful rough guide for more than 40 years. Confusingly, this seems to be the tensile modulus E, so the shear modulus G, which is more relevant to adhesives, needs to be 0.1. However, plenty of people, including myself have stated that G~0.3. Given that it's only a rule of thumb, let's not get too worried about the exact value. There is a surprising variation in the quoted values of the Dahlquist criterion with 0.3MPa being common and other values are clearly wrong such as 10⁶ Pa and even, in some cases, 105Pa which is an unfortunate misprint. Dahlquist’s original statement was 3x10⁶ dyne/cm² and it is strangely common to see this quoted as 3x10⁶ dyne/cm² (0.1MPa), even though 3x10⁶ dyne/cm²=0.3MPa - though maybe they were implying the conversion from E to G.

The Dahlquist G is really a G' and you now know never to think about G' without thinking about timescales. For putting a PSA onto a surface the timescales are typically 1s, so the relevant G' for a room temperature PSA at 25°C is ~1Hz, a convenient temperature and timescale for routine G' and G'' measurements in rheometers or DMAs.

An alternative formula, suggest by Prof Michele Ciavarella of Politecnico di Bari, is more directly related to real-life measurements of surface roughness

G_c=Wλ_q/(4R_q²)

Here λ_q is the RMS wavelength and R_q is the RMS height of the rough surface. The advantage of the Ciavarella formulation is that both parameters are standard, real-world values found on more advanced surface roughness measurement devices, rather than the idealised values in the original formula. The formula can be derived from Eq.5, 8 and 10 in this paper². Those who want more detail can find it in this pdf note from Ciavarella & Papangelo. Note, however, that the use of λ_q in the app is for pragmatic reasons. The precise relationship between this and the λ₀ used in the theory is not clear.

Clearly there is more to PSA than room temperature, 1Hz applications. Dahlquist is a middle-of-the-road criterion. For a more profound way of thinking about good PSA designs we need the next app - the Chang Window.