Real Adhesion
Quick Start
The intermingling discussed in the Hysteresis app is useful for adhesion but rarely enough. We need entanglement, where the polymer chains literally tangle like a ball of string. The stronger the entanglement, the stronger the adhesion.
The measured adhesion depends on Σ, the density of entanglements, and L, the length of the entanglemnts. As you increase the values you find seriously strong adhesion, in the N/m range rather than mN/m.
If you tried this experiment with a normal JKR setup you would probably break it. The app shows the principle. In practice you would use an AFM or a nanoindenter to do the measurements.
Real
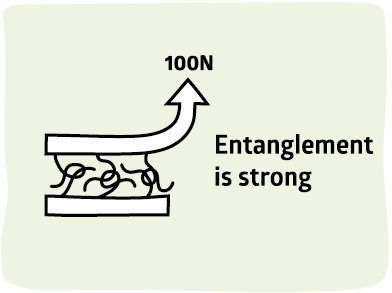
We've seen that the more intermingling there is between the two surfaces, the stronger the adhesion. The effect is a factor of 10 over surface adhesion - useful but not strong enough for the real world. In this page we find a way to increase adhesion by at least another factor of 10 - giving us really strong adhesion.
In earlier versions of the app, the unloading curve was shifted upwards, without an explanation of how it got there. More satisfactory is this newer version where the width stays constant on unloading till the force/width balance is restored to what the full curve would have been.
The key to success is entanglement. Imagine two pieces of string that are merely intermingled. It doesn't take a lot of force to pull them apart. Now imagine them in a tangle - as you pull they wrap around each other, making it more and more difficult for you to separate them. Indeed it becomes impossible to separate them - you have to pull till the string breaks. It turns out that this is exactly what happens when you get strong adhesion - the polymer chains are entangled and adhesive failure occurs when the bonds break.
There is a remarkably simple formula that describes the extra adhesion from entanglement. If surfaces with a chain density of Σ/nm2 , an entangling number of polymer repeat units of N and a U is the energy/repeat unit to break a bond then the extra adhesion, G, is given by the Lake & Thomas formula:
G= ΣNU
This is exactly the same formula as the intermingling formula of the previous chapter. The only thing that has changed is that U is now 350kJ/mole instead of 3.5kJ/mole. In reality the value for Σ will be somewhat smaller (maybe a factor of 2-10 because it is hard to get a lot of tangles), so the boost in adhesion (for the same length of entangled chains) is not the full factor of 100, but it's still a big boost. In other words the important formula is:
Adhesion = Entanglement
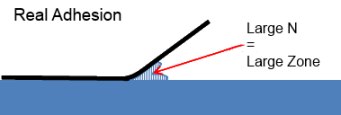Visually, the Lake & Thomas formula is shown in the figure. By having a large value of repeat units, N, you have to stretch a large amount of polymer before there is bond breakage. This dilutes the effective crack propagation force. If there is some plastic deformation as well then that absorbs even more energy.
To explore this effect we keep the same settings as before (including an intermingling adhesion ~0.41J/m2) and allow the length and density to apply to entanglement rather than intermingling:
With such strong adhesion, the JKR loading curve is hardly visible! That simply re-emphasises how dramatic the effect of entanglement really is.
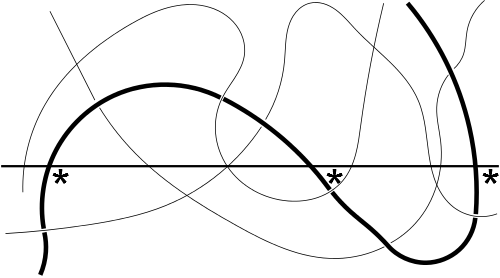The definition of entanglement in a polymer is remarkably simple: polymers are entangled if at any interface the chain crosses it 3 times or more. This can be illustrated by the image made famous by Prof Richard Wool of U. Delaware.
Although this "3 crossings" principle is well-known, it is harder to know how many crossings are in your particular polymer. The MWt at which you get 3 crossings is called the "critical entanglement weight" Mc. To get good entanglement you want a low value of Mc. Mc depends in a complex manner on the way the polymer does or does not coil on itself and on the number of side-chains which add MWt but don't help entanglement. At this point it is just necessary to understand the 3 crossings rule and the fact that different polymers have very different Mc values.
What about chemical adhesion?
So far we've spoken only about polymers intermingling and entangling. It turns out scientifically that if instead of an entangled system you have a chemically cross-linked system the results are identical - the Σ value is now the cross-link density (across a virtual interface plane) rather than the entanglement density. To appreciate why there is no difference (in terms of adhesion) between entanglement and cross-linking imagine two sets of string. In the first set, the pieces of string are arranged so that there is a tangle at a given average spacing. In the second set, instead of a tangle the pieces of string touch each other at the same places as the tangle but are stuck together with a strong glue. When you try to pull the two sets of strings apart the results are identical. Cross-linking really is identical to entanglement in terms of adhesion. (Of course cross-linking has other effects, for example adding chemical resistance to a system).
We are now ready to bring everything together and model the effects of all the relevant parameters.
