Shear Testing PSA
Quick Start
Our mantra is that Adhesion is a Property of the System. It should be little surprise, then, that the standard shear test for PSA usually measures peel. Everyone does the shear test, everyone knows the formula, but few know that the reasons most results don't match the formula is that the failure (for a good PSA) is in peel mode. The other two shear tests are real shear, but are less well-known and look at somewhat different issues.
Classic shear test

Because PSA gain strength by being able to flow (G'') there is always a trade-off between peel strength and shear strength. The time to fail is given by: `t=(L^2wη)/(2mgh)` where L is the length, w the width of the sample, η is the viscosity, m is the mass attached to the peel strip, g is gravity and h is the thickness of the adhesive. Many exceptionally strong PSA when peel tested will prove to be weak against shear. The Feldstein equation in Basics showed, for example, that peel strength increases with low viscosity η but as the equation shows, the time required to fail a shear test decreases with lower η. Similarly, a doubling of the adhesive thickness h doubles the peel strength but halves the time to fail a shear test.
PSA Classic Shear
As it happens, this simple model for shear is often much to pessimistic, predicting shear failure long before real failure happens. The cross-linked nature of many PSA often transform an apparent shear failure into a real peel failure - i.e. the rate of downward creep depends on (effectively) a 180° peel at the upper interface.
'Small' strain shear test
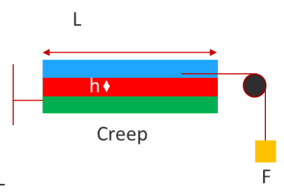
The Burgers model discussed in the Ideal PSA allows us to look more closely at the early stages of the shear test - i.e. the creep measured in a static shear tester. Assuming you're already familiar with the fact that the behaviour is a combination of fast and slow processes, depending on the relative elastic and viscous components, then we can simply state that the extension, γ, for a given stress τ (=F/(w.L)) at time t for the given moduli G1, G2 (using G instead of E because now we are talking about a shear modulus) and viscosities μ2 and μ3, is given by:
`γ=τ/G_1 + τ/G_2(1-exp(-tG_2/μ_2))+(tτ)/μ_3`
PSA Small Strain Shear Test
The effect of the τ/G1 is usually negligible given that values for G 1 are typically near the GPa range. The general creep is the t.τ/μ 3 term which dominates in longer times. The initial portion of the curve therefore depends on whether G 2/μ 2 is small (long slow curve) or large (almost instant effect); the inverse of the ratio is the "retardation time" tr which is calculated. The calculated strain is in terms of the thickness of the adhesive layer. So a stretch of 50μm for a 50μm film would be 100%. As the theory starts to break down over 100% the calculation stops at whichever of 100% strain or your chosen t max is reached first.
Squeeze test
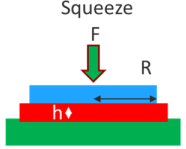
We worry about whether our PSA will ooze out under pressure. The squeeze tester pushes a plate of radius R with a force F against a sample of adhesive of thickness h and viscosity η. The thickness of adhesive ht after time t is given by Stefan's equation:
`1/(h_t^2)=1/h^2+(4Ft)/(3πR^4η)`
As the app shows, the rate of squeeze declines rapidly with thickness because of the squared term - halving the initial thickness of a PSA reduces the initial ooze by a factor of 4. Obviously the radius of the compressing plate has a very large effect.
PSA Squeeze Test
As we will discuss in the Strength section, just about everything to do with PSA is a compromise - which is why they are so hard to get right.


