Weak and Strong
Quick Start
Here is proof that Adhesion is a Property of the System. The same pieces of rubber, tested in three different ways require a force to separate them that differs by a factor of 1000! The formulae show why. Peel depends (for this system) only on surface energy and the width of the sample. In Lap and Butt joints the modulus (and thickness) of the rubber dominate the measured force.
Just play with the four parameters and see how the separation forces differ wildly from each other. Then see the formulae to understand why.
Weak & Strong
There is a key quote by Gordon in his wonderful book Structures: or why things don't fall down: "It turns out that the total energy needed to break all the bonds to any one plane or cross-section in most technologically relevant materials is very much the same and does not differ widely from 1J/m2".
What this means is that the strong chemical bonds holding glass together give, when measured carefully, a Work of Adhesion of at most 1J/m2. Given that a weak stickynote has W=40J/m2 it seems that glass is very weak. Which it is if you manage to get a crack in it. Similarly, to break apart all the ionic bonds in a crystal of salt requires something like 0.4J/m2 because ionic bonds are weaker than chemical bonds.
Yet if you try to pull glass (or salt) apart you find that it takes much more than 1 (or 0.4)J/m2 to do so. A material which in terms of Work of Adhesion is objectively weak is, in terms of ease of pulling apart, objectively strong. How can these two truths be reconciled?
As with so much of testing, the result depends on how you do the test. If you drive a wedge into glass or salt then it turns out that the value of the "strength" that you measure is the pure work of adhesion, W, <=1J/m2, just as if you had peeled them apart in an ideal test. Other ways of applying the force give different results:
The force required to peel across a width b is `F=W.b`. |
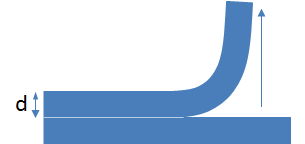 |
But if you test by pulling in a
lap joint then a lot of what you are doing goes into stretching the material. And the ability to stretch it depends on its modulus E. It turns out that the measured value of `F=2bsqrt(WEh)` where h is the thickness of the sample being pulled.
|
 |
For a button of material of radius a being pulled vertically, i.e. a
butt joint the force needed to break it is `F=sqrt(10πWEa^3)`.
|
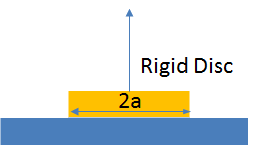 |
These formulae (slightly simplified) are well-known but are best found in Prof Kevin Kendall's marvellous Molecular Adhesion and Its Applications: The Sticky Universe, Springer, 2001 along with their simple but powerful derivations.
Use the app to compare the measured "peel" and "pull" for a given work of adhesion, W, width, b, (or radius a=b/2), thickness, h, and modulus, E. In addition a pseudo failure stress is calculated as F/Area where area is assumed to be b*b for peel and lap and πa² for butt. It is a pseudo value because for, say, the lap joint the forces are not equally spread across the joint, something described in the respective peel, lap and butt apps.
Here are a few typical values of E for some standard materials:
| Material | Modulus GPa |
|---|---|
| Copper | 110 |
| Aluminum | 70 |
| Steel | 200 |
| Glass | 70 |
| NaCl | 40 |
| Epoxy | 2.5 |
| PI | 2.5 |
| PET | 4 |
| PC | 2.5 |
| PMMA | 2 |
| PE | 0.8 |


