Butt Test
Quick Start
The butt joint is a great example of how NOT to think about adhesion. Countless papers report a force F to break an area A so give a value of F/A MPa. Butt joints do not fail evenly across the area. They fail with forces concentrated at the edges, and small defects, or small deviations from a 90° pull can cause large concentrations of forces and earlier failure. So the quoted MPa values are meaningless.
Playing with surface energy W, A and modulus E may not cause much surprise, but the thickness of the adhesive layer, d, has an unexpected effect: the thinner it is the better.
Butt Test
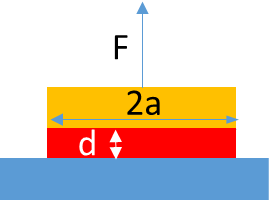
The Butt joint is not the greatest of joints and the Butt test is not the greatest of tests. The idealised version of it from Kendall's The Sticky Universe is included here because it is another reminder that testing doesn't test what you think its testing. A related, but different pull (Butt) test is described in the Weak and Strong page.
Take an adhesive of modulus E (and therefore a bulk modulus, `K=(3E)/(1-2ν)`, where ν is the Poisson ratio, taken here to be 0.33), a Work of Adhesion W and thickness of d. Assume the joint has a cross-sectional area of A (i.e. πa2). Then the force needed to pull it apart is given by:
`F=A.sqrt((KW)/d)`
Famously this shows that an adhesive of zero thickness requires an infinite force, so not only do you save on cost of adhesive but you get a very strong joint. Clearly the assumptions behind the model break down at very low values of d. But for small thicknesses, such joints can be amazingly strong - provided you stay strictly in pull mode. If you pull with a slight tilt then the bond will break (in this idealised system) with a peel force of ~W.A½.
For guidance, a typical strong adhesive (such as an epoxy) has a modulus ~1GPa.


