Dewetting
Quick Start
Many printing techniques produce a "dot" which is effectively a cylinder of height hc and radius rc. For a non-wetting ink, this cylinder is unstable and wants to retract to a spherical cap of radius rsc at the equilibrium contact angle θe. The speed of dewetting depends a bit on surface tension σ and viscosity η, but it mostly depends on θe via a temporary angle during dewetting.
The default conditions are for a large drop used by the team who developed the theory. Printed dots are much smaller and dewetting times are super short - an issue discussed later.
Dewetting
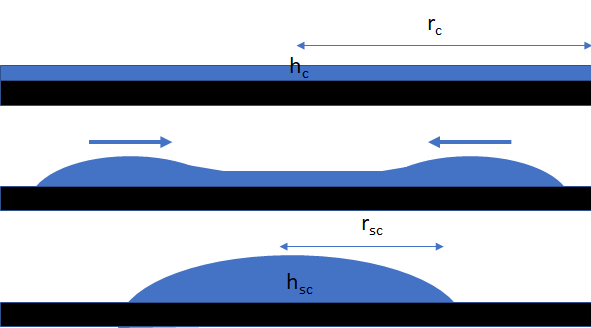 If you have somehow created a thin dot of liquid onto a surface (e.g. via offset, flexo or gravure printing) it can be considered as a small cylinder of height hc and radius rc. If the liquid has a static contact angle of θ which is greater than 0, then the cylinder will de-wet into a spherical cap of height hsc and radius rsc. Using an ingenious method of pinning a liquid using dielectrowetting and then releasing the drop by turning off the field, a team at Northumbria and Nottingham Trent universities1 were able to study the dewetting process and show that a relatively straightforward analysis described the process very well, with only a modest set of reasonable assumptions.
If you have somehow created a thin dot of liquid onto a surface (e.g. via offset, flexo or gravure printing) it can be considered as a small cylinder of height hc and radius rc. If the liquid has a static contact angle of θ which is greater than 0, then the cylinder will de-wet into a spherical cap of height hsc and radius rsc. Using an ingenious method of pinning a liquid using dielectrowetting and then releasing the drop by turning off the field, a team at Northumbria and Nottingham Trent universities1 were able to study the dewetting process and show that a relatively straightforward analysis described the process very well, with only a modest set of reasonable assumptions.
As the diagram shows (the default conditions are from the paper so you can compare the app to the experiment), dewetting is not the opposite of wetting. Instead a rim of liquid moves inwards at (as it happens) a near-constant velocity until the rims collide and then the drop relaxes to a spherical cap. The velocity is given by:
v=kθ³σ/η
where k is a constant depending on the velocity, the width of the rim and the dewetting slip length assumed here to be 1nm.
The plot shows the decreasing radius relative to the original, the increasing contact angle relative to θ, and the increasing height relative to hsc. The plot changes from linear to exponential when the rims meet in the middle.
The calculation of the constant k is complex because it depends on the width of the rim, the contact angle and the capillary number which itself depends on speed, so there are a number of numerical loops to get a self-consistent solution.
The dewetting speed problem
If you put in any typical offset or flexo dot height (4μm) and radius (100μm)and a respectable contact angle such as 30°, you find that the dewetting takes place with remarkable speed. This basically tells us that printing would always show massive dot loss, at least in terms of area measured with a microscope (the amount of ink is the same so the measured values would be OK). I have never seen any evidence for such an effect. So is the theory wrong or is there another factor? One can imagine that for complex offset inks the theory might be inadequate at high speeds, but flexo inks aren't usually too far from Newtonian, so this seems implausible.
My personal view was that there is, under these timescales, a big difference between advancing and receding contact angles, with the receding values remaining close to 0 in these timescales. So there is no driving force for dewetting as long as the equilibrium contact angle isn't too high. I had the chance to consult dewetting expert Dr Stein Kuiper about this and he confirmed that pinning from "chemical" interactions and from micro-roughness are both strong effects - so receding contact angles are indeed much lower than advancing ones. He also explained that smooth silicone surfaces dewet quickly because of the smoothness and because there is little chemical interaction.
But still, I need to publically admit that I've been wrong about the need for lower contact angles in printing. Against the usual arguments, I've been correct: you don't need a wetable surface in order to get full contact during an offset or flexo print splitting event. And I've always admitted that contact angle affects pinholing. But, I'd never seen a dewetting argument and had never even thought of the issue.
On the positive side, instead of worrying about contact angles (which tell us that we still have a dewetting problem even if we have a generally acceptable equilibrium angle such as 30°), we can concentrate on what things (polymers and surfactants, plus microroughness) will give us a very low receding contact angle.
The expert guidance through the complexities of the solution by Dr Rodrigo Ledesma-Aguilar is warmly acknowledged, as is the support from Prof Glen McHale.
1Andrew M. J. Edwards, Rodrigo Ledesma-Aguilar, Michael I. Newton, Carl V. Brown, Glen McHale, Not spreading in reverse: The dewetting of a liquid film into a single drop, Sci. Adv. 2016; 2 : e1600183


