Permeability Calculations
Quick Start
My heart sinks if I have to do permeability calculations or convert OTR or WVTR units or change WVTR at one temperature and %RH to different ones. And I'm not alone. This app does all three of those jobs and has helped many of us in multiple ways because it brings some sanity to a totally confusing mess of units, measurements and errors in the literature.
Each time I use the app after some time away from it, I ask myself if it could be easier to use and understand. So far, I've not found a reason to change it because the logic is there and it works reliably, exposing confusions in the literature and getting me (and others) to the right answer time after time.
Are you confused by calculations of permeation through barrier films? Confused by Permeance versus Permeability, don't know what a Barrer is, find your calculations differ by a factor of 5 or have no idea how to go from `(cm^3.cm)/(cm^2.s.mmHg)` to `(g.m)/(m^2.day.atm)`? If so, you are not alone. A wonderful paper1 by Prof Cooksey and colleagues at Clemson University showed that lots of people were equally confused, including textbook authors. The 10's of 1000's of visitors to this page are equally confused and as you'll see below, this page itself had errors (now fixed!).
By tracking down the confusions, the Cooksey paper showed it was possible to create four clear recommendations - which are implemented here. I've added a 5th and 6th.
- Be clear whether you want to know TR which is Transmission Rate which is the actual amount that gets through a unit area of a real sample, or whether you want to know the Permeability, P, which is the amount that will go through a unit area of unit thickness. In other words, TR is the real quantity which depends on both material properties and their individual Thicknesses, L, and P is the intrinsic property of each material. Incidentally, the paper points out that to say "permeability rate" is the same as saying "rate rate".
- Be clear that it is generally agreed that "permeance" is the same as "transmission rate", so is not the same as permeability. If you meet "permeance" out of context, you have to be very careful because sometimes they mean transmission rate and sometimes permeability.
- Be clear about what units you are using. Permeability is a nightmare of units. In the first app we sneakily avoid the issue so it is easier to concentrate on the calculations. But a fully generalised unit converter is provided below for your convenience.
- For multi-layer calculations, use the formulae below in their specific format to avoid confusion and to get the right answer every time.
- For unit interconversion, use this app, or, if you write your own conversion spreadsheet, check it with this app which, by now, is reliable thanks to corrections over the years.
- Assume that the values you find in published results are wrong till you've checked them carefully. I have spent many hours using this assumption and although it's nice to find papers where everything is correct, they are a minority. Even if their values are correct, the units they quote might be wrong or (see below) confusing or you can't be sure if they mean transmission rate or permeability because their own terminology is inconsistent.
Transmisson Rate/Permeability Multilayer Interconversions
 To calculate the total Transmission Rate from individually known TR values (i.e. each layer at its given thickness has a TR known to you experimentally).
To calculate the total Transmission Rate from individually known TR values (i.e. each layer at its given thickness has a TR known to you experimentally).
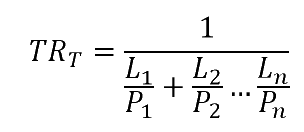 To calculate the total Transmission Rate from individually known P values (i.e. the experimental or literature property of each material) with known thicknesses L of each layer.
To calculate the total Transmission Rate from individually known P values (i.e. the experimental or literature property of each material) with known thicknesses L of each layer.
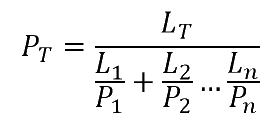 To calculate the total Permeability (i.e. normalised to a standard thickness) from individually known P values (i.e. the experimental or literature property of each material) with known thicknesses L of each layer and total thickness LT of the barrier.
To calculate the total Permeability (i.e. normalised to a standard thickness) from individually known P values (i.e. the experimental or literature property of each material) with known thicknesses L of each layer and total thickness LT of the barrier.
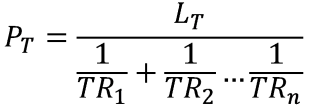 To calculate the total Permeability (i.e. normalised to a standard thickness) from individually known TR values (i.e. each layer at its given thickness has a TR known to you experimentally) along with the known total thickness LT of the barrier.
To calculate the total Permeability (i.e. normalised to a standard thickness) from individually known TR values (i.e. each layer at its given thickness has a TR known to you experimentally) along with the known total thickness LT of the barrier.
The table lets you select up to 6 layers, each with a given thickness in whatever units you happen to like, e.g. mil or μm. You can then enter a P and get a TR for that thickness or, in the final two columns, enter a TR and get a P. The PT and TRT are then calculated for each mode. The answers aren't necessarily the same as the primary inputs (P and TR) are different.
There is one more compliction. TR may be measured at, say, 20% oxygen or 50%RH in which case the calculated P values (which are normalised to 100% of the gas) would be 1/5 or 1/2 of their true values. So you need to enter %TR, the test value, in order to get the right TR from P or the right P from TR.
The calculations only work if the thickness units for P are the same as the units chosen for thickness. If your units for P give values such as 3.2e-14 just enter the 3.2 and assume the e-14. If there were just one or two units for P then the app would handle them, but there are so many, with such bizarre mixtures of US and metric systems that it's not worth trying.
For a table of typical P values, click : . As of April 2020, there is a bonus table of values at the bottom of this page.
Multilayer TR to P or P to TR Converter
| %TR | ||||||
| Use | Thickness | P--> | TR | | | TR--> | P |
| | | ||||||
| | | ||||||
| | | ||||||
| | | ||||||
| | | ||||||
| | | ||||||
| LT | PT | TRT | | | TRT | PT | |
| | |
Permeability Units Converter
| Mass | Length | Area | Time | Pressure | ||
| From | ||||||
| To | ||||||
| MWt | Seconds |
| ThicknessFrom Units | TRFrom Units | ThicknessTo Units | TRTo Units |
We have the definition that `Permeability=(Mass."Length")/(Area.Time.Pressure)`, though surprisingly the resulting unit is Time - i.e. the unit is simply "seconds" (for fun the value in Seconds is always provided - it's a sort of universal standard). The problem is that everyone chooses different values of Mass, Length, Area, Time and Pressure, leading to 1000's of potential units (currently the app can convert between 3360 different units). Rather than try to list all possible units, choose from the common variants of each unit and the converter will do the appropriate calculation. There is no restriction - if you wish to mix US and metric units (a surprisingly common, if bizarre, thing to do) the converter will not object. For those who need cm³ (ml)as the Mass unit, the MWt of the gas is needed, 2 for hydrogen, 18 for water, 28 for nitrogen, 32 for oxygen. For those who have values in Barrers, the units to enter are `(cm^3.cm)/(cm^2.s.mmHg)`, plus a factor of 10-11.
As a bonus, if you specify the thickness in the original From units, the Transmission Rate, TR, is calculated in original and in To units, along with Thickness in the To units.
Note: up to 22 March 2018 there was an error of 324 too large in conversion of g water to cc of vapour. Thanks to Steve Rose who spotted and reported it! Then Sébastian Gaucel pointed out on 11 Jan 2019 that the conversion for oxygen and water were made at STP (i.e. 0°C) rather than at NTP (25°C), which is more generally applicable. If you have done previous calculations they will differ by a factor of 22.4/24 or 24/22.4.
Then thanks to Peter Palomaki for pointing out on 10 April 2020 that I had an error (now fixed) in the Thickness and TR conversion calculation. Then in April 2024 Er-Chien Wang pointed out different error, now fixed, with the same those conversions. Again, thanks!
Different industries adopt different "rationalisations" of the units. For example some see that units such as `(g.m)/(m^2.s.atm)` can be simplified by dividing top and bottom by m, giving `g/(m.s.atm)`. This is correct but very confusing because the units no longer make intuitive sense. Even worse, those who like pressures in units of MPa note that `MPa=(MN)/m^2` and those `m^2` cancel out, giving units of `(g.m)/(MN.s)`. Whilst also "correct" this is also totally confusing. As mentioned, the actual unit is Seconds and if people quoted this (it's provied here) as an extra sanity check, life would be much easier.
To convert TR simply make sure that the Length units and the Pressure units are respectively the same (it doesn't matter what they are) so that they cancel out. A typical conversion would be g/(m².day) to g/(100in²/day) with "per atmosphere" implied.
WVTR/MVTR at different T and %RH
| WVTR | T°C | %RH | |||
| In Atm | In mm/Hg | In MPa | |||
| T°C | %RH | WVTRcalc |
There's an unfortunate complication with water. WVTR is usually stated as wt/(area.time), e.g. g/m².day with no reference to the pressure. So it is impossible to do the above calculations without the ability to know what the pressure component is. There's no elegant way to do this, so make do with the following.
Enter the WVTR in the units of your choice, the temperature and RH of test (typically 38°C and 90%RH). The outputs are the TR values in your original units plus the respective pressure units of atm, mm/Hg, MPa.
There is also an extra row for entering a different T and %RH so that you can get an estimate of what the WVTR would be at those settings. This is useful for comparing different claimed values in the literature. Is a WVTR of 20 at 38/90% much better or worse than a value of 5 at 23/50%? Of course, water vapour effects aren't always linear between different tests (higher T and RH can cause extra effects), but it's at least a starting point for comparison.
In April 2020, it was pointed out to me by Patrick Galler that these calculations didn't take into account the change in permeability with temperature of the polymer itself. He also mentioned that if you know the activation energy, EA of polymer diffusion you could calculate the effect via exp(EA/RT). I don't have EA values for typical polymers to incorporate into this app. However, if you go to my Diffusion Coefficients app on my Practical Solubility website you can find estimates of how diffusion coefficient changes with temperature for a number of common polymers. Just multiply the value from the app here by the ration found from that app to get a better estimate. He also pointed out that I'd accidentally squared the effect of the new RH. That has been fixed.
For those who want to see the interplay of T, RH, Absolute Humidity etc. the Water Vapour app is a handy tool.
Bonus Table
There is an excellent guide to OTR and WVTR science produced for Homeland Security by the Pacific Northwest National Lab, Water Vapor Permeation in Plastics by Paul E. Keller and Richard Kouzes. Interestingly, the guide cites this website for those who get confused by units. With kind permission from the authors here is a selection of data they painstakingly assembled. Notice the wide variation in reported values which, as the authors comment, may be due to variations in measurement temperatures as well (my comment) as the complexities and errors typical of these measurements.
| Polymer | P O2 cm³·mm/m²·d·atm | P Water g·mm/m²·d |
|---|---|---|
| Acrylonitrile - Styrene | 19.7- 102 | 2.0 - 6.3 |
| Acrylonitrile Butadiene Styrene (ABS) | 19.7 - 102 | 2.0 - 6.3 |
| Sabic Cycolac ABS | 39.3 | 5.88 |
| BASF Terluran ABS Film | 45.6 - 81 | 3.1 |
| Dow Acrylonitrile ABS Films | 47 - 102 | 2.0 - 6.3 |
| Styrene-Acrylonitrile (SAN) | 20.2 - 50.6 | 2.0 - 2.5 |
| Dow Chemical Tyril SAN | 31.5 - 39.4 | |
| BASF Luran 378P | 20.2 - 30.4 | 2.0 - 2.5 |
| Polystyrene (PS) | 98.5-171 | 0.8 - 3.9 |
| Dow Trycite Oriented PS Film | 98 - 138 | 1.3 |
| BASF AG Polystyrol 168 N GPPS Film | 101 | 1.2 |
| Rubbers | 7.88 - 4330 | |
| Polyisoprene | 4320 | |
| Butyl rubber | 7.88 - 85.4 | |
| Methyl rubber | 11.8 - 722 | |
| Natural rubber | 1530 - 1580 | |
| Neoprene | 1640 - 2630 | |
| Silicone rubber | 3940 - 4330 | |
| Polyvinylidene fluoride/Hexafluoropropylene | 95.2 | |
| Polyamides (PA) "Nylon" | 0.3 - 23.6 0.24 - 125 | |
| Nylon 6 | 0.394 - 2.50 | |
| Nylon 6,6 | 2.23 | |
| Nylon 6,9 | 2.3 | |
| Nylon 6,10 | 1.31 | |
| Nylon 8 | 3.81 | |
| Nylon 11 | 7.88 | |
| Nylon 12 | 23.6 | |
| Capron Nylon | 7.5-7.9 | |
| DuPont Selar Amorphous Nylon | 2.16 - 7.07 | 0.47 - 0.55 |
| DuPont Selar Blends with Nylon | 0.3 - 5.9 | |
| Honeywell Plastics Capron Nylon 6 | 0.24 - 5.9 | |
| UBE Industries Nylon 6 | 65 - 125 | |
| Polyamide Imide (PI) Resins | 4.3-22.8 | |
| Polyamide Imide (PI) Polymers | 0.1-58.7 | |
| Polyetherimide (PEI) | 10.0-53.0 | 2.3-3.0 |
| Polyethylene (PE) | 26.3 - 453 | |
| High Density Polyethylene (HDPE) | 26.3 - 98.5 | 0.1 - 0.24 |
| Mid Density Polyethylene (MDPE) | 98.5 - 210 | 0.4 - 0.6 |
| Low Density Polyethylene (LDPE) | 98 - 453 | .39 - 0.59 |
| Polyethylene Naphthalate (PEN) | 0.5 | .096 - 4.2 |
| DuPont Mylar Films (no metal) PEN | 1.13 - 1.18 | 0.38 - 0.57 |
| Mitsubishi Hostaphan PEN | 0.9 | |
| Fluoroplastics | 1.18 - 394 | |
| Polychlorotrifluoroethylene (PCTFE) | 2.76 - 5.91 | |
| Fluorinated ethylene propylene (FEP) | 295 - 394 | 0.087 |
| Polyvinyl fluoride (PVF) | 1.18 0.83 | |
| Polytetrafluoroethylene (PTFE) | 222 - 387 | 0.0045 - 0.30 |
| Polyvinylidene Fluoride (PVDF) | 5.52 | |
| Ethylene Vinyl Alcohol (EVOH) | 0.01 - 0.15 | 0.8 - 2.4 |
| Polyvinylidene Chloride (PVDC) | 0.00425 - 0.57 | 0.025 - 0.913 |
| DOW Saran PVDC Films | 0.00425 - 0.00625 | |
| Polyvinyl Chloride (PVC) | 3.28-394 | 0.94 - 0.95@38C |
| PVC, rigid | 3.28-39.4 | |
| PVC, plasticized | 39.4-394 | |
| Poly Propylene (PP) | 35 - 377 | |
| Llyondell Basell Adflex PP | 35 - 377 | |
| Polyoxymethylene (POM) | 5.9 | |
| Polycarbonate (PC) 'Lexan' | 71 - 124 | |
| Dow Calibre PC | 91 - 124 | |
| Bayer Makrolon PC | 71 - 81 | |
| Polymethylpentene (PMP) | 7.8 - 91 | |
| Polymethyl Methacrylate (PMMA) | 5.8-6.7 | 1.7 |
| Lucite Diakon PMMA | 5.8 1.7 |
1Kay Cooksey et al, Predicting Permeability & Transmission Rate for Multilayer Materials, Food Technology, 53, 60-63, 1999

