Capillary Fill Time

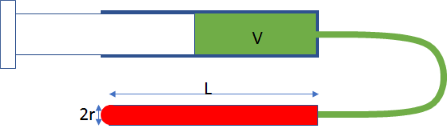It seems simple enough. You have a capillary of length L and radius r that you want to flush out with a fresh liquid of viscosity μ from a syringe. Let's suppose, as in the diagram (which is not to scale!), that the liquid in the syringe is green and that in the capillary it is red. You take the first syringe you can find, say, 1ml and push and expect to see the red liquid immediately disappear and the capillary to be filled with green. But nothing seems to happen.

Surprisingly, it's not that the syringe is blocked; it's the laws of physics instead. We commonly assume that water is incompressible - and this is a good assumption most of the time. In fact it has a bulk modulus, E, of 2.2GPa, so if you apply a pressure P to a syringe of volume V then the reduction in volume is given by:

`V_"change"=(PV)/E`

By the Poiseuille law, that pressure, P gives a flux, Q through the syringe such that:

`V_"change"=(8QLμV)/(πr^4E)`

Finally, that volume change is flux times time,t, i.e.:

`V_"change"=Qt`

So now we can find out how long it takes to flush out the capillary:

`t=(8LμV)/(πr^4E)`

For larger values of r, or smaller syringes, the time is so short that we don't notice it. But the default setting of a 1ml syringe and a 1μm radius capillary shows that the time is in hours! That's why we have apps. Something which, instinctively, should take no time at all can be shown, if you choose the wrong setup, to take minutes or hours.

Note that the bulk modulus is assumed to be that of water and is fixed as 2.2GPa. If you happen to know the value of your specific fluid, you can adjust the calculated time as 2.2/E_real, a lower modulus giving an increased time.