Marangoni (& Rayleigh) Number Calculator

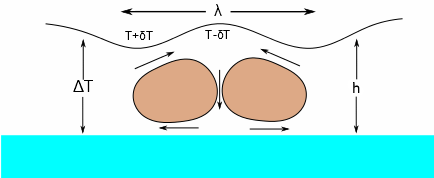The Marangoni Number, Ma, captures the tendency of a coating to spontaneously generate surface-tension driven flows that, at an extreme can produce a coating of perfect hexagons (Bénard Cells) and in general make your coated/printed layer (especially in the case of ink-jet) unacceptable.

The equation is simple and the app performs the calculation for you:

`Ma = -(δσ)/(δT)(hΔT)/(ηκ)`

What this means is that a flow is driven by a surface tension gradient that is larger for large values of the rate of change of surface tension with temperature (δσ/δT) and, of course, a large temperature gradient (ΔT) between the surface and base of the coated/printed layer. The thicker the coating (h), the worse the effect. The Bénard Cells are shown being created by the flow. The surface tension is higher when T=T-δT and lower when T=T+δT (i.e. surface tensions decrease with temperature, which is why Ma is characterised by the term -δσ/δT), hence the direction of the arrows of flow. The wavelength λ of the cells is given by λ=2πh/√(Ma/8).

You can reduce Ma by having a high viscosity (η) and a high thermal diffusivity (κ). The viscosity effect is obvious. A high thermal diffusivity means that the effect of the temperature gradient is rapidly diminished.

Typical values might be 0.1 mN/m/°C for δσ/δT, 10μm for the thickness, 10°C for the temperature difference and 5cP for viscosity. Most of us can get good numbers for these values. The problem is κ. Using the convenient units of mm²/s, some values are Water=0.14, Ethanol=0.07, Acetone=0.083. For most alkanes, alkenes & simple aromatics, κ=0.08-0.09.

Fortunately my colleague Dr YAMAMOTO, Hiroshi on his amazing Pirika site has created a wonderful scheme for estimating κ from chemical structure (along with δσ/δT and μ if you haven't been able to measure them) so you can automatically get an estimate of your Marangoni number (in units of L=1m and ΔT=1) or use the κ value with your known δσ/δT and μ in this app. See Pirika Marangoni Estimator and also explore the many other offerings on the Pirika site.

Concentration driven Marangoni

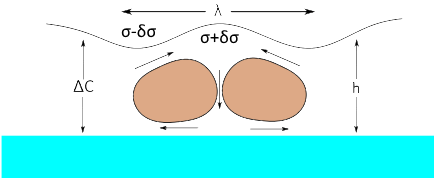Although it has always been known that Marangoni can be driven by a concentration-surface tension gradient, it has classically been less studied, though it is more generally important for coatings such as paint. The formula and the calculations here follow the approach of Saranjam¹ and colleagues. The key equation involves the change of surface tension with solvent concentration, δσ/δC, the change of concentration over the thickness of the film, ΔC, the thickness, h, the viscosity, η, (note that these two inputs are the same as the temperature-dependent calculation) and the diffusion coefficient of the solvent through the matrix, D.

`Ma = (δσ)/(δC)(hΔC)/(ηD)`

For typical paint films in the 100s of μms, with surface tensions changing typically by 1mN/m for a 10% change in solvent concentration², with a 10% concentration difference and with values of D~1e^-6> cm2/s then the value of Ma is very large. As the paper shows, this can quickly reduce for relatively thin coatings where the concentration gradient quickly reduces while the viscosity quickly increases. So a transitory set of Bénard cells can appear then disappear as Ma reduces rapidly.

Reducing Marangoni

What value of Ma do you require? "As low as possible" is a glib answer. It depends how quickly the coating dries/solidifies - if that is a rapid process then the Marangoni flow has no time to cause problems, but if it is slow then you need a low Ma to give a perfect coating. The official answer is that if Ma<80 then there is no instability. In reality instabilities can be found for values at least as low as 40, but in the app anything above 80 is highlighted in red as a warning. Whether the same value of 80 appplies to the concentration gradient effect seems to be debatable.

Clearly reducing thickness and increasing viscosity helps with all Marangoni. For the temperature-driven effect, a solvent with a lower temperature coefficient will help. For concentration-driven effects, the Diffusion coefficient is key: though how you rationally control this independently of the viscosity is an interesting question.

One obvious trick for aqueous coatings and thermal Marangoni is to add a surfactant to reduce σ and, in all probability, to reduce δσ/δT. However, this adds complications of its own as surfactants have their own dynamic behaviour and can make things positively worse. And adding a solvent such as ethanol to reduce σ leads to the risk of concentration-gradient driven flow if, for some reason, the ethanol starts to evaporate slightly quicker at one point. This takes you from the first to the second type of Marangoni. Debates can reach theological intensity about which effect (thermal gradient "thermocapillary" or concentration gradient "solutocapillary") predominates (and what name to give it - Marangoni, Gibbs...) in real cases where concentration gradients arise because an involatile component is being coated/printed in a volatile solvents. Gibbs' name appears because any tendency for a component to form a monolayer at the surface (Gibbs isotherm) can calm (uniform layer) or worsen (local areas) the effect.

This brings us to the choice of solvents when solutocapillary Marangoni is likely. If a single solvent is being used (typical of the literature) then the effect will reduce/disappear if the solvent is changed from lower to higher surface tension, reducing δσ/δC. If (as is usual in real life) we have solvent blends then, as with water/ethanol above, if the faster-evaporating solvent has a lower surface tension then that can produce a gradient, independent of the polymer. By ensuring that the more volatile solvent has a higher surface tension, then (during the crucial early stages) δσ/δC will be negative, stabilizing the system. This strategy can only be taken so far. If the viscosity is still high when the high surface tension solvent has gone then we are back in the domain where a higher surface tension is better. Clearly the ideal is to ensure that the system viscosity becomes high enough to quench the Marangoni before the faster-evaporating solvent has gone.

As a personal anecdote, I once had a coating with weird streaks. Looking down the microscope, at the start of each streak was a hexagon, so Marangoni was playing a significant role. By changing the co-solvent from ethyl acetate (more volatile than the main solvent) to butyl acetate (less volatile) completely fixed the problem.

Rayleigh-Bénard

A further confusion arises because the Rayleigh-Bénard effect gives rise to similar visual effects. The general phenomenon is the same but it is driven by density changes between hot and cold (or dilute and concentrated) regions. If, for simplicity in the app we assume that density is ~1 so that kinematic viscosity = dynamic viscosity then the critical number, Ra, for the Rayleigh-Bénard instability is:

`Ra=(αgh^3ΔT)/(ηκ)`

The differences with Marangoni are the use of the thermal expansion coefficient, α, which is typically ~0.007 for liquids, the addition of the acceleration of gravity, g, and the h³ dependency. Systems are unstable when Ra>1000 (a value of 1708 is sometimes quoted). Because of the h³ term, Rayleigh-Bénard effects only become significant in thick (mm-scale) fluids (try this with the thickness slider which is logarithmic), which is why we tend to look for them in pans of water rather than in coatings.

Surfactant Effects in Aqueous Systems

These are not included in the app because the effects are complex and confusing. Those who like to use the word Gibbs in this context will see surfactants producing a surface adsorption effect which will, in general, resist curvature and stabilise the system, increasing the critical Marangoni number. But there are plenty of literature examples where surfactants make things worse because they set up their own potent concentration and surface tension gradients. There are cases where surfactants up to their CMC are stabilising then become destabilising. Whether the surfactant is soluble or insoluble, small molecule or polymeric makes a difference. Famously, surfactants can even cause slow-drying surfaces to level, but then carry on in the opposite direction to produce an un-levelling.

A common experience is that some of the acetylenic surfactants give good levelling. My interpretation (see DST-Choice) is that these are poor surfactants at high concentrations (their CMC is high) that swamp the surface then evaporate before they can add extra complications.