Nanoindentation
Quick Start
We all know what modulus is but fewer of us know what hardness is, other than as some vague word. Here we show how a nanoindenter can give you both modulus and hardness which are not at all the same thing.
The first time I used a nanoindenter and found out about hardness, it was a revelation. Myself and my colleagues learned more about our system from that one day on the nanoindenter than we'd known for years previously.
There's no short cut here, other than saying that modulus is about elastic resistance, while hardness is about plastic resistance, i.e. the ability not to permanently deform under pressure.
Nanoindentation
Many nanocoatings are used as tough, scratch-resistant surfaces. Those creating the formulations need to optimise and tend to think that high modulus is the key to success. A high loading of silica or alumina nanoparticles can certainly deliver high modulus, and ceric oxide can provide UV resistance as well. But it is often observed that there is (beyond a minimum level) little correlation between modulus and "toughness". With hindsight this lack of correlation is obvious. To be resistant to, say, scratching, the coating must not give plastic (permanent) deformation. By definition, modulus is all about elastic (temporary) deformation. What is needed is a measure of resistance to plastic flow - and the key parameters are hardness, plastic depth and elastic recovery, with hardness being the key.
All these parameters are measured using a nanoindenter. A sharp (Berkovich) tip is pushed into the coating with an increasing force and the displacement is measured. The force is decreased and the displacement continues to be monitored.
The app is backwards - you input the modulus, E, and hardness, H, (along with a maximum load Pmax and a Poisson ratio, ν, typically 0.3) and the nanoindenter trace is simulated, and the extra parameters such as elastic recovery are calculated. The idea is to give a feeling for what a real-world experiment might look like.
The calculated hardness is based on the definition of
Hardness = Force/Contact_Area.
Obviously the assumptions behind the creation of the nanoindenter curve are only approximations. The aim is to build up your intuitions of how things change, not to do hardness calculations, which your nanoindenter will happily perform for you, once you can get hold of one.
The calculation assumes a diamond indenter of modulus 1141GPa, ν=0.07. The contact area is calculated using standard Berkovich parameters.
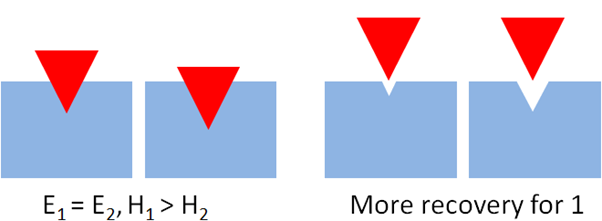Hardness is a very important parameter that many of us are unfamiliar with. The definition, Hardness = Force/Contact_Area seems to make little sense. However, a simple example helps make it clear. The same tip is pushed with the same force into materials with the same modulus E1=E2 but with different hardnesses H1 > H2. The tip enters further into 2 and on withdrawal it is clear that the tip has left a bigger permanent impression on the substrate - i.e. there has been more plastic flow and less elastic recovery. Finally, we can see that the contact area with the tip is higher for 2 than for 1, so Force/Contact_Area is less for 2 than 1, so the Hardness is lower for 2. It's as simple as that!
