Rheology

This is not intended as a course on rheology. If you would like a quick guide then you can download the Abbott Rheology Guide The aim here is to "remind" you of some key issues that apply to coatings.

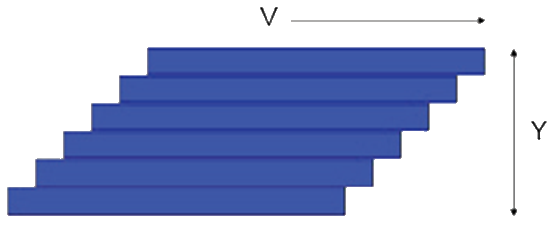The starting point is a pack of cards of height Y and with a force τ moving the top card with a velocity V. There is friction between the cards and the card on the bottom is immovable. For a given inter-card friction, the force τ will need to double if V is doubled for obvious reasons. It also has to be doubled if Y is halved because the velocity gradient, V/Y is much steeper so each card feels more of the influence of the fixed card. If the inter-card friction is called η then τ=η.V/Y. Now substitute "streamline" for card and we have the equation for the force required to push the surface of a liquid of thickness Y at velocity V. V/Y has units of (m/s)m = 1/s and is the "shear strain rate" which is given the symbol γ̇. Rheologists tend to call this "strain rate" and the rest of us call it "shear rate" or just "shear". Because shear rate is in s^-1 and shear stress is in Pa (i.e. force/area = N/m²) then viscosity is in Pa.s.

We know that the above relationship was derived by Newton and fluids which obey that law are Newtonian fluids. The cause of viscous drag is familiar to those who drive in busy traffic. If a driver in a slow lane moves into a faster lane that causes the cars behind to slow down to accommodate the new arrival. For ordinary molecules in liquids their random movement between streamlines causes the same slowing down (viscous drag). When polymer molecules are concerned, if one part of the polymer is in one streamline and another part is in a different streamline then the polymer starts to be stretched, causing a bigger drag between streamlines. However, with faster streamlines the polymer chains tend, on average, to become more and more aligned with the flow so they cause proportionally less drag between the streamlines. So higher shear leads to lower viscosity in many polymer systems. For such non-Newtonian systems the graph of viscosity versus shear rate can be conveniently described using the Cross formula:

`η = η_"inf"+(η_0-η_"inf")/(1+(α+γ̇)^n)`

where tη_inf is the viscosity at (essentially) infinite shear, η₀ is the viscosity at zero shear and α and n are fitting constants. Most of us are used to seeing viscosity plotted versus log shear rate. It is therefore a shock to see it plotted versus linear shear rate. Rheologists prefer to plot shear stress versus shear rate (with and without logs) and this is even more of a shock. It's worth playing around with both the Cross model parameters and the different ways of looking at the same data. See below for the Power Law option

Different parts of your process create different shear rates and therefore different viscosities. It is easy to estimate the shear rate for any given process. Squeezing an adhesive at 5cm/s from a nozzle that is 0.5cm diameter gives a shear rate of 5/0/5=10 while the same adhesive being squeezed as a 10μm layer at 0.1m/s gives a shear rate of 0.1/10^-5=10⁴. Enter the estimated shear rate and the relevant viscosity and shear stress are calculated.

Although the Power Law (or Ostwald Law) curve is essentially useless (the Cross model is much more realistic and general), it remains popular so if you click the Show Power Law option you can see its effect. The equation (slightly modified to be consisten with η₀ and η_inf) is:

`η = η_"inf"+(η_0-η_"inf")γ̇^(n-1)`

The equation blows up γ̇<1 so the value is fixed at η₀ for these values. The reason some people use the power law curve is that they can provide a single number, sometimes called "P Ostwald", to use on, say, a product data sheet.