Stefan's Law

How a drop of liquid deforms under squeeze pressure affects both printing (dot gain) and UV embossing (residual layer).

The same basic formula with its dependence on starting thickness h1, viscosity η and drop radious R works for both, with the R4 dependence dominating things, followed by the h² term. The force F is important for both, though for printing we use the nip pressure.

An alternative view of squeeze flow of a drop of adhesive can be found at Drop Squeeze within Practical Adhesion

Stefan's Law for Printing

h1 nm
Speed m/min
R1 μm
η cP
Pressure MPa
F on dot
t on dot
R2
Dot gain R
Dot gain A

Stefan's Law for UV embossing

h1 nm
h2 nm
R μm
η cP
F N
t

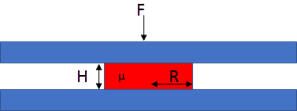Stefan Squeeze TheoryIn both printing and UV embossing, a feature of radius R and thickness h1 is squashed with a force F and will go to thickness h2 after a time t that depends also on viscosity η. The time, t, taken is given by Stefan's law (this is a different Stefan from the black body radiation formula):

`t=(3πR^4η)/(16F)(1/h_2^3-1/h_1^2)`

For the printing situation, you apply force F for time t on a dot with radius R1, with an initial thickness h1. From this you can calculate h2 and, by conservation of volume you can calculate R2 and the % in area gain.

`1/h_2^2=1/h_1^2+(16Ft)/(3πR_1^4η)`

`R_2=sqrt((h_1R_1^2)/h_2)`

Rather than input F and t directly, we take a (hopefully) measured nip pressure in MPa (pressures in the 0.5-1MPa range are normal) and a known printing speed V. F is MPa times Dot_Area (πR²) and t=2R/V.

We can take 3 lessons from this in terms of dot gain. Confusingly there are three possible measures: the gain in radius, the gain in printed area and, not shown here, the value quoted in dot gain curves1.

  1. Halving pressure, Doubling viscosity, Doubling speed each cause a 1.4 decrease in radius dot gain or 2x reduction in the area (measured) gain. Offset's super-high viscosities are clearly an advantage compared to flexo, though flexo pressures will be lower.
  2. In the formula, larger dots have a larger F (R²) and t (R) giving an R3 increase, outweighed by an R4 decrease, giving a 1/R dependence. The net result is that halving the radius increases gain by 1.4 (or 2 for area).
  3. Halving the ink thickness halves the radius gain or reduces area gain by a factor of 4. So going to a more pigmented ink requiring a smaller thickness gives significant dot gain benefits.

UV embossing

In UV embossing a feature of radius R is pushed into a UV coating of thickness h1 and viscosity η with a force F. The idea is to get down to a thickness of h2 as quickly as possible, with h2 ideally being close to zero.There are four key points for UV embossing:

  1. Going to 0 thickness requires infinite time - so UV embossing always leaves a residual thickness and you never get infinite dot gain.
  2. Halving the desired residual quadruples the time required for UV embossing
  3. Doubling the radius of the feature gives a 16x increase in time.
  4. Viscosity and Force only have a linear effect so are not so critical.

So UV embossing is easy with lots of small features and an acceptance of a significant residual thickness. It is hard if broad features with little residual are required.

1If your plate has a 20% dot and it prints as a 30% dot, then the convention is to say that this is a 10% dot gain, even though it is clearly a 50% increase relative to its original area.