Hardness
Quick Start
Pressing a square pyramidal tip with a known load into a surface and measuring either the depth or the width of the resulting permanent indentation mark gives you the Hardness via a simple calculation.
Credits
The Nanoindentation app shows the fancy version of this using an expensive nanoindenter.
Hardness
//One universal basic required here to get things going once loaded
window.onload = function () {
//restoreDefaultValues(); //Un-comment this if you want to start with defaults
Main();
};
//Main() is hard wired as THE place to start calculating when inputs change
//It does no calculations itself, it merely sets them up, sends off variables, gets results and, if necessary, plots them.
function Main() {
//Save settings every time you calculate, so they're always ready on a reload
saveSettings();
//Send all the inputs as a structured object
//If you need to convert to, say, SI units, do it here!
const inputs = {
m: sliders.Slidem.value,
D: sliders.SlideD.value * 1e-6, //μm to m
};
//Send inputs off to CalcIt where the names are instantly available
//Get all the resonses as an object, result
const result = CalcIt(inputs);
document.getElementById('Data').value = result.Data;
if (result.plots) {
for (let i = 0; i < result.plots.length; i++) {
plotIt(result.plots[i], result.canvas[i]);
}
}
//You might have some other stuff to do here, but for most apps that's it for Main!
}
//Here's the app calculation
//The inputs are just the names provided - their order in the curly brackets is unimportant!
//By convention the input values are provided with the correct units within Main
function CalcIt({ m, D}) {
const g=9.81
let HPts=[],HPPts=[], HMPts=[], i=0, DC=0
const HPa=1.854*m*g/(D*D) //Pa
const HV=1.854*m/(D*D*1e6) //g/mm^2
const depth=1e6*D/(2*1.414*2.475) //to μm
for (i=0;i<=2*m;i+=2*m/100){
DC=Math.sqrt(1.854*i*g/HPa)
HPts.push({x:i,y:DC*1e6})
DC=Math.sqrt(1.854*i*g/(HPa*1.1))
HPPts.push({x:i,y:DC*1e6})
DC=Math.sqrt(1.854*i*g/(HPa*0.9))
HMPts.push({x:i,y:DC*1e6})
}
//Now set up all the graphing data detail by detail.
let plotData = [HMPts,HPts,HPPts], lineLabels = ["-10%","H","+10%"]
const prmap = {
plotData: plotData, //An array of 1 or more datasets
lineLabels: lineLabels, //An array of labels for each dataset
hideLegend: false, //Set to true if you don't want to see any labels/legnds.
xLabel: 'Mass&kg', //Label for the x axis, with an & to separate the units
yLabel: 'D&μm', //Label for the y axis, with an & to separate the units
y2Label: null, //Label for the y2 axis, null if not needed
yAxisL1R2: [], //Array to say which axis each dataset goes on. Blank=Left=1
logX: false, //Is the x-axis in log form?
xTicks: undefined, //We can define a tick function if we're being fancy
logY: false, //Is the y-axis in log form?
yTicks: undefined, //We can define a tick function if we're being fancy
legendPosition: 'top', //Where we want the legend - top, bottom, left, right
xMinMax: [0,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
yMinMax: [0,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
y2MinMax: [,], //Set min and max, e.g. [-10,100], leave one or both blank for auto
xSigFigs: 'F1', //These are the sig figs for the Tooltip readout. A wide choice!
ySigFigs: 'F0', //F for Fixed, P for Precision, E for exponential
};
//Now we return everything - text boxes, plot and the name of the canvas, which is 'canvas' for a single plot
return {
Data: "H = " + (HPa/1e9).toPrecision(3) + " GPa, Vickers = " + HV.toPrecision(3) +" h =" +depth.toPrecision(3) + " μm",
plots: [prmap],
canvas: ['canvas'],
};
}
 Hardness is a very important parameter that many of us are unfamiliar with. The definition is:
Hardness is a very important parameter that many of us are unfamiliar with. The definition is:
`"Hardness" = "Force"/"Contact Area"`
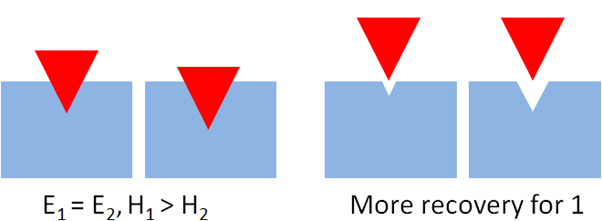
This seems to make little sense. However, a simple example helps make it clear. The same tip is pushed with the same force into materials with the same modulus E1=E2 but with different hardnesses H1 > H2. The tip enters further into 2 and on withdrawal it is clear that the tip has left a bigger permanent impression on the substrate - i.e. there has been more plastic flow and less elastic recovery. Finally, we can see that the contact area with the tip is higher for 2 than for 1, so Force/Contact_Area is less for 2 than 1, so the Hardness is lower for 2. It's as simple as that!
An expensive Nanoindenter will give you all the detail you require so you can sort out elastic and plastic deformations. Here we use a simple Vickers indenter, applying a known force, and measuring the indent we have made. For metals, you can just apply the load, remove it and measure. For polymers you probably need to apply the load for, say, 2 minutes and wait, say, 1 minute before measuring. The first wait allows time for plastic flow and the second wait allows time for elastic recovery. You can experiment with different timings to gain insights into your specific material.
You can buy a Vickers (micro)hardness machine that will do all this for you. Or, to allow versatile hardness measurements, you can buy 3 Vickers tips, attach them as a triangle to a plate and apply them with a known total weight (~0.3 to 2 kg) to your surface. You get 3 datapoints to give you some statistical certainty.
Some machines can measure the depth but others, and the simple devices, need a microscope to measure the diagonal width, D of the indent created by a force F. The tip is at an angle of 136°, giving a half angle of 68°. Here we use the mass and diagonal as the input data. The formula is:
`H=1.85F/D^2`
To translate between D and the depth, h, we use
`h=D/(2sqrt(2)tan(68)`
If F is in kg and D is in mm, the calculated H is the Vickers hardness. If F is in N and D is in m then H is in N/m², i.e. Pa. Typically the values are large (because D is typically 10s of μm) so are quoted in GPa.
When you do a measurement you might wonder about whether you've chosen the right mass and/or the accuracy of the measured value. The graph shows how D varies with mass (the scale changes to 2x your input mass) and how D might change for a +/- 10% variation in hardness.


