HSP Basics
Quick Start
HSP are three numbers that provide a lot of practical formulation power. Here we show where they come from, why they work and give you the HSP values of ~1000 chemicals.
Another simple way to look at the basics is via the Lattice Theory app.
Like, as we all know, attracts like. So if we have a formula for "like" we can judge the solubility of a polymer in a solvent or the compatibility of a polymer and plasticiser or the stability of a nanoparticle in a solvent dispersion by how alike they are.
It starts with evaporation
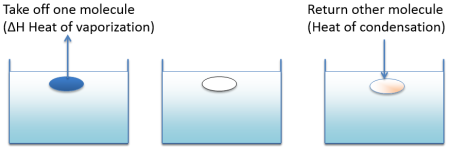 It takes energy (enthalpy of vapourisation) to evaporate a solvent. You get all that energy back when you condense it. If you evaporate a portion of a solvent and then condense in an equal volume of a different solvent, if the two solvents are alike then the energy cost of doing this is minimal and the solvents are miscible. If they are very different then energy in and out don't balance and the miscibility is low.
It takes energy (enthalpy of vapourisation) to evaporate a solvent. You get all that energy back when you condense it. If you evaporate a portion of a solvent and then condense in an equal volume of a different solvent, if the two solvents are alike then the energy cost of doing this is minimal and the solvents are miscible. If they are very different then energy in and out don't balance and the miscibility is low.
It's more precise to talk of the cohesive energy, E, of a solvent, i.e. how much energy is required to break it apart into gas molecules. If E is broken into 3 components of Dispersion, Polar and Hydrogen-bonding then we get:
E = ED + EP + EH
We are generally not familiar with cohesive energy. Instead we know the latent heat of vaporization Hv, R the universal gas constant, and T the absolute temperature . The relationship between them is:
E =HV-RT
Cohesive energy is not so useful on its own. Bigger molecules in a molecular series, not surprisingly, have bigger cohesive energies. To scale them so that molecules in a series are more comparable we need the cohesive energy density which is obtained by dividing by molar volume V:
E/V =ED/V + EP/V + EH/V
The cohesive energy density is more conveniently handled in terms of the solubility parameter δ where δ²=E/V. This gives us the classic formula for Hansen Solubility Parameters where the total parameter, δ, is broken into δD, δP and δH for Dispersion, Polar and Hydrogen-bonding:
δ² = δD² + δP² + δH²
The units of solubility parameters are MPa½. Older references use (cal/cc)½ which are a factor of 2.0455 smaller.
The measure of "like"
The HSP Distance between two molecules, conventionally called Ra, is the measure of how alike they are. The smaller Ra, the more likely they are to be compatible. The famous formula, used for 40+ years is:
Ra² = 4(δD1-δD2)² + (δP1-δP2)² + (δH1-δH2)²
The factor of 4 in front of the δD has aroused controversy for decades but plausible theoretical reasons and overwhelming experimental evidence show that it is valid. Conveniently it makes HSP plots into nice spheres. If from measurements of "good" and "bad" solvents you can define a sphere of radius Ro which contains all the good solvents, then you can define a Relative Energy Difference, RED, which tells you where you are in solubility space:
RED=Ra/R0
HSP Values
If you know the HSP of your solvents, polymers, plasticisers, pigments, nanoparticles, bio-system... then it is very easy to use the Distance formula to understand solubility, swellability, dispersability, permeation and so forth. Here is the standard Hansen set in convenient searchable/sortable format. Click on the top of any column to sort ascending then descending, type a part of a chemical name or a CAS number to find relevant chemicals.
| Chemical | CAS | δD | δP | δH |
|---|
If there is no solvent with the right balance of HSP, cost, safety, odour etc. (and these days it is very hard to find such solvents) you can create your own by mixing solvents, using the rule that the HSP of the mix is the volume-weighted average of the HSP of the components. And Hansen's method of measuring HSP of unknowns via simple good/bad tests with a range of solvents and fitting to a Sphere is not hard to do. The Excel spreadsheet HSP_Calculations.xlsx allows you to try out many of the basics. The famous Pirika site from Dr YAMAMOTO, Hiroshi provides lots of insights into HSP along with a number of handy apps for carrying out calculations.
Confusion over values
There are lots of HSP values available via the internet and in the academic literature. But many of the published values are suspect as they use different methods (van Krevelen, Hoy etc.) to estimate HSP values and they are not necessarily compatible with each other. Many estimation methods give nonsensical values. For example, some published values on polyvinylpyrrolidone showed δP values <1 which is simply not credible for such a highly polar side-chain! There have even been academic papers where some values were quoted in the now standard units of MPa½ alongside values in old-fashioned units of (cal/cm²)½ - which made attempts to fit the data very unsatisfactory. To convert from the old units, multiply by 2.0455.


