Bancroft's Rule

HLD theory makes it superfluous to use an old-fashioned approximation. But Bancroft's "rule" (more a rule of thumb) is much used in the surfactants world so cannot be ignored. The rule is simple, "The phase in which an emulsifier is more soluble constitutes the continuous phase." So water-soluble surfactants tend to give o/w emulsions and oil-soluble surfactants give w/o emulsions.

There are many complementary explanations for the rule, but my favourite is the following:
During the emulsification process, drops of oil and drops of water are formed indescriminately as their formation process does not depend strongly on anything - as we saw in the Emulsion Surface Area app, the energy required to create the surface area is orders of magnitude smaller than the energy typically supplied to create an emulsion. Bancroft's rule kicks in when drops collide. Suppose we have a water-soluble surfactant and two water drops in oil start to collide. For them to merge it is necessary for the surfaces to deform. Any deformation is resisted by the elasticity of the surfactant shell around the drop. But the elasticity of a water drop containing lots of surfactant is rather small - as two surfactant molecules are pulled apart there is plenty of surfactant just below the surface ready to move in to fill the gap - so the two drops have essentially no elasticity and readily collide and merge.

But two oil drops meeting don't have the luxury of a ready supply of surfactant in the drop, so they are much more elastic. They are much more likely to bounce apart and in fact the so-called Taylor velocities of the two drops decrease rapidly as they approach and they might not touch at all, whereas the Taylor velocity of the water drops stays high.

There is little point in discussing the complexities of Taylor velocities - the simple elastic explanation is good enough for most of us. In any case, there are many exceptions to Bancroft. The simple argument works OK for 50:50 o:w but most of us tend to use rather low levels of the dispersed phase (which don't need so much surfactant) and it is well-known that you can get the "wrong" phase when you are far from 50:50. The Fish Tail app shows how HLD-NAC theory copes with changes in the o:w ratio.

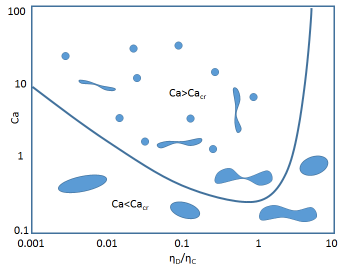Relative viscosities of the two phases are also important and the "critical viscosity ratio" rule can kick in so that the "wrong" phase is the only one that can form an emulsion. The rule is that for shear flow typical of an emulsion dispersion head, you cannot make drops form unless the "capillary number", Ca is greater than a given value Ca_crit.

Ca=η_c.G.R/γ

Here η_c is the viscosity of the continuous phase, G is the velcoity gradient from the mixer, R is the desired radius of the drop and γ is the interfacial tension. Ca_crit depends on the ratio of the viscosities of the dispersed and continuous phase η_d/η_c. So you have to put in plenty of power to get drops at all. By going to a low γ you get a high Ca, which is why you can get good emulsion formation when HLD=0, though of course the emulsion is not stable unless quickly quenched to HLD<0. But if η_d/η_c > 4 then no amount of power can create drops. However, if we redefine the phases as being "anti-Bancroft" then the ratio is <0.25 so an emulsion can form. So high viscosity oils with an aqueous-soluble surfactant might still form w/o emulsions because the o/w form simply cannot be created.

If extensional flow is used (e.g. a membrane emulsifier) this viscosity ratio rule does not apply. So the "same" emulsion formulation with a water-soluble surfactant might give w/o in a conventional homogenizer and o/w from a membrane emulsifier.