Foam Elasticity

Foam elasticity is an important aspect of its resilience - an elastic foam is likely to survive longer than an inelastic one. The theory outlined here which indicates a maximum elasticity is somewhat controversial (such maximum effects are rarely seen) but it contains all the basics and is interesting in its own right. The theory is from Wang & Yoon¹.

The elasticity of a material is stress/strain, i.e. the force required (stress) to change the dimensions by a certain amount (strain). For foams the elasticity, E, depends on how the surface tension γ changes with film surface area A. This can also be expressed in terms of surfactant concentration, c:

`E=2A(δγ)/(δA) = 2A(δγ)/(δc)(δc)/(δA)`

For those who like to think in terms of "effects" the restoring force is the Gibbs or Marangoni force (experts will argue which is which) - the bigger the Marangoni force the more elastic a bubble is.

From the basic insight of what E is, it is possible to define E in terms of measurable quantities: surfactant concentration c; the bubble film thickness h; the maximum surface excess (adsorption density) Γ_m which is discussed in Basics; the equilibrium adsorption constant K; RT, the gas constant times temperature:

`E=4RT.(γ_m^2K^2c)/(h(1+Kc)^2+2γ_mK)`

The key values Γ_m and K can be obtained from fitting the standard plot of γ v c to the Langmuir-Szyszkowski equation as discussed in Basics.

`γ=γ_0-RT. Γ_mln(1+Kc)`

The maximum elasticity is obtained at a concentration c^* given by:

`c^"*"=sqrt(1+2Γ_mK/h)/K`

K can be calculated from the CMC and Δγ=γ₀-γ_c where γ_c is the equilibrium surface tension at or above CMC

`K=(Exp((Δγ)/(RT.Γ_m))-1)/"CMC"`

For this app RT is assumed to be that at 25°C, i.e. 2479J/mol. Γ_m is in units of µmole/m² and CMC is in units of µM. h (thickness) is in nm. The concentration plot for the graph is logarithmic in M from 1E-6 to 1E-1.

Given that (see below) h typically varies only from, say, 30 to 50nm (or from 5 to 10nm) and that Γ_m varies only from, say, 1 to 10 and that RT varies little over a typical temperature range from 25-60°C, the big effect on elasticity is K. This can vary from 10 to 10,000,000. So to get good elasticity (only one of the key parameters for a good foam) concentrate on ensuring a high value of K via a low CMC and low γ_c!

It is well-known in foam formulations that small additions of molecules such as myristic acid can have a large effect on elasticity. The main surfactant creates the foam in the first place, then the additive displaces the main foamer from the interface to create a more solid wall.

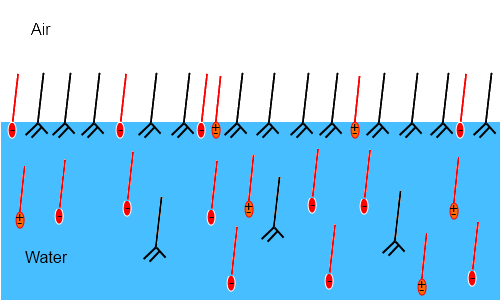
In this image² the small % of myristic acid (black, neutral) in the formulation displaces most of the SLES (red, negative ionic) and CAPB (orange, zwitterionic) and forms a tough, elastic surface ideal for resisting Oswald ripening and antifoams.

As mentioned in Basics, there are some ways to calculate Γ values and, therefore, elasticities of mixed surfactants based on the properties of the individual surfactants along with some interaction parameters. It seems to me to be rather easier to measure the elasticities of the mixtures (via "standard methods") than to attempt to rationalise them via formulae which are perhaps OK for mixing surfactants of the same class but which become intractable when applied to more realistic mixtures.

What values should be used for h?
It is surprisingly easy to make a suggestion for values of h. For ionics choose ~30nm and for non-ionics choose ~5nm. Where do these values come from? See the DLVO section for the equilibrium values of ionics and non-ionics which depend on charge and steric stabilisation respectively. But how long does it take to reach equilibrium value? Apparently "a few seconds". Or, to put it another way, all the key research groups seem to assume that h is the equilibrium value for most practical foam experiments on Ostwald ripening, drainage or rheology.

But surely h depends on the pressure inside the bubble? Yes it does, and those with plenty of time and patience can record the thickness v pressure curves for a given surfactant system. But halving the radius and, therefore, doubling the pressure generally has only a modest effect (e.g. 10% reduction) on h, so in general we need not worry too much.