Roll-up and Eötvös Number

A lot of mysteries around roll-up can be neatly resolved by looking at the Eötvös Number, E, of the system. This is one of the important "dimensionless numbers" used in fluid science and is simply the ratio of Gravitational to Surface Tension forces. Where g is gravity then for a drop of oil of density difference (with respect to water) of Δρ, characteristic radius R and IFT between water and oil of γ then:

`E = (ΔρgR^2)/(2γ)`

The approach here is based on a series of papers by Dr Jaideep Chatterjee of Unilever and specifically uses the 'arc-length' methodology from the paper¹ that combines the elements of the other papers. He prefers E to the equivalent Bond number which is the same without the factor 2 along the bottom.

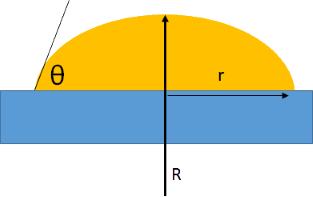R is defined as the radius of a spherical cap drop of the given volume and with a pure contact angle θ that ignores interfacial tension effects. Another radius, r, is defined at the interface with the surface. In real life, r will change over time and as the IFT changes but to make a difficult problem tractable, r is assumed to be constant (pinned contact line). As the drop deforms the actual contact angle differs from the pure contact angle θ and is shown in the calculation as θ_calc.

It turns out that there is a critical value of E, E_crit, below which the drop will never separate by roll-up or snap-off. This critical value depends strongly on the contact angle, θ, of the oil with the surface. It needs a very large value of E to remove a drop with a low contact angle.

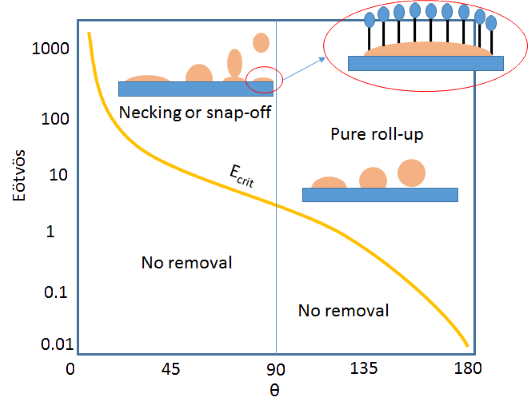The diagram shows the E_crit line plus my interpretation of some of the trends that follow from the theory. On hydrophilic surfaces (e.g. cotton with a high oil/surface contact angle,) just about any surfactant can generate the modest value of E needed to give roll-up. On hydrophobic surfaces (e.g. polyester with a low oil/surface contact angle) it requires a very large E.

Because large values of E are more likely to allow roll-up (especially on hydrophobic surfaces), and because we can do little about Δρ and R, the only thing we can do is control γ. A typical γ from a typical surfactant with a typical oil is 4mN/m. Only when HLD~0 does γ reduce to something like 0.1. So the chances are that when a typical surfactant gives E below the critical value (especially on hydrophobic surfaces such as polyester) the detergency will be low whilst the 40x increase in E (4-->0.1mN/m) is enough for gravity to force the drop to separate spontaneously.

In a real detergency situation agitation is provided to avoid the reliance on the relatively mild gravitational force. But the point is still valid - a typical IFT may give little help to oil removal while an optimised system with a low IFT will give much more effective cleaning.

To bring the ideas alive, the drop shape is calculated by integrating the Young-Laplace equation via a Runge-Kutta 4th order method as described in the paper. The problem is that the integration involves a key value, the curvature at the top of the drop, which is unknown till the drop shape is calculated. So the method makes a guess about the curvature, integrates to get the shape and volume of the drop, then tries again with a different curvature value till the volume is calculated correctly. Like many numerical algorithms, there are conditions where the algorithm can go wrong. Please ignore obviously erroneous results.

What is striking is that the drop shape alters very little within the range of "normal" IFTs. Only when you go to really low IFTs, i.e. those found when HLD~0, do you see significant drop shape changes which go, of course, with a significant change in the Eötvös number and, therefore, a significantly increased chance of roll-up with or without snap-off.

One other mystery is explained by this approach. When snap-off occurs, a drop remains on the surface. It is often seen that this drop also snaps off relatively quickly. Intuition suggests that once a large amount of oil has gone from a drop it would be much harder to persuade the remaining oil to move. The R² dependency of E suggests a strong effect. But suppose the initial drop is 5μl and E=1. If 4μl of the initial drop snap off for the remaining 1μl E=0.34, a significant but not massive reduction. The reason is that R depends on the volume V^0.333, so the reduction in E is a factor of 2.9 not 5.

The Stable and Unstable labels give a rough indication about whether the drop shape (or the calculation) is valid. When it's valid then the drop is likely to be stable, when it's invalid the drop is likely to fall off via roll-up or snap-off. The value of E_crit is from a simplified theory and you will find that things go unstable within a factor of 2 of that value.

The Chatterjee papers are plotted in terms of dimensionless X and Y values (the real values scaled by R). Here the dimensional values are used. The plot is scaled so that the x and y axes are equal. This allows you to compare the images to what you see in your favourite roll-up paper.