Spinning Drop Tensiometer
Quick Start
Via HLD-NAC you can arrange to get very low IFT values. Standard measurement techniques are useless so you have to use a spinning drop tensiometer. They are elegant and simple in principle but fiddly in practice. Recent models are said to be much more user-friendly.
SDT
When you have a surfactant system that is working effectively and delivering a low interfacial tension (IFT) , you need a subtle measurement technique to get an accurate value of the IFT.
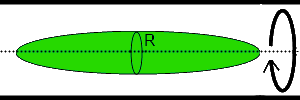
The most common technique is the Spinning Drop Tensiometer (SDT) where a drop of oil in a narrow tube elongates as the tube is spun along its long axis. The app shows it in action, the explanation is below.
This description of how it works is an attempt to put the physics into simple language. Take a narrow tube containing your surfactant solution and syringe in a drop of the oil. The oil drop will be spherical. Imagine squeezing the top and bottom of the drop. Naturally it will spread sideways into a cylindrical shape. The more you squeeze it, the longer the cylinder and the smaller the radius of the cylinder. And, of course, for a given squeeze, a lower interfacial tension will give a longer cylinder because there is less surface tension resistance.
The trick in the SDT is that the squeezing is done simply by rotating the tube around its long axis. The denser material (the water) is pushed out more strongly by centrifugal force than the oil. Because the water wants to be on the outside, that means that it pushes the oil towards the centre of the spinning tube. In other words, just spinning the tube squeezes the oil drop in a nice controlled manner.
It turns out that the Radius, R, of the squeezed cylinder depends on the interfacial energy, γ, the difference in density, Δρ and the angular velocity ω. To calculate σ from the measured Radius and the known density difference and spin speed the classic Vonnegut formula is used:
`γ=(Δρω^2R^3)/4`
The derivation of this formula can be found at the excellent FIRP documents site at the Universidad de los Andes Venezuela
Play with the values to see the (simplified) graphics of the drop. In this app the IFT is an input and the Radius and output, but of course in a SDT the Radius is measured and the IFT calculated. The formula fails when the width of the drop is <4*Radius. The graphics do not attempt to show realistic drops around that limit. The app readily shows that for the technique to work you have to be within a reasonable rpm, density difference and IFT. At one extreme the drops are effectively spherical so no measurement is possible and at the other extreme the drops are very thin and difficult to measure accurately.


