Foam Fractionation

We know from the elasticity discussions that a surface active agent (now we are deliberately not using the word surfactant) comes to the air/water interface. Implied, but not explicitly shown, is that the surface excess Γ (the concentration of the agent at the interface in mol/m²) depends on the concentration, C (mol/l) according to an isotherm which in turn depends on a maximum value of Γ, Γ_m (where m is said to mean "monolayer") and a parameter K so that:

`Γ=(Γ_mKC)/(1+KC)`

We also know that when a foam is generated, much of the water drains away between the bubbles. So all that surface excess of the agent is sitting in an environment with rather little of anything other than air. So if the foam can be extracted then broken, it is likely that the concentration of the surface active agent in the resulting fluid is considerably higher than the original. An example is that the concentration of protein in Guinness beer is 0.3% but the concentration of protein in the foaming head is 73%. When this is done methodically to remove a surface active agent from a bulk liquid the process is called foam fractionation. To continue the focus on alcoholinc drinks, the aroma of champagne is considerably enhanced because the bubbles fractionate the aroma chemicals from the bulk and when they explode at the surface they eject the aroma into our olfactory system.

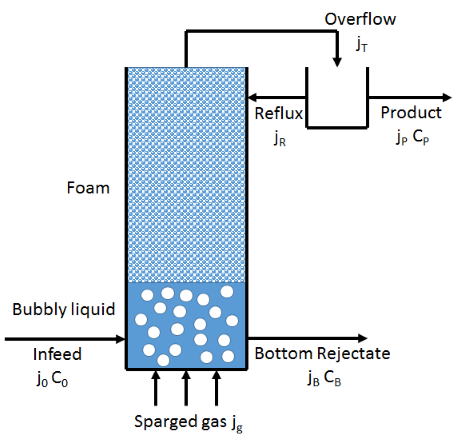The standard reference on foam fractionation¹ is by Stevenson and Li and I am grateful to Drs Stevenson and Li for their kind support in creating this app. Of necessity this app simplifies many points that are explained at length in the book.

As per the diagram (based on Fig 6.3 in the book) we assume that air is being bubbled into a column of liquid and the bubbles of radius r (Sauter mean for those who attend to such details) rise with a superficial velocity j_g. [The "real" velocity is j_g/Φ where Φ is the volumetric gas fraction in the bubbles. So when φ is 0.1 the real velocity is 10xj_g.] Liquid with surface agent concentration C₀ is being pumped in at a rate j₀ and the depleted liquid at concentration C_B is removed from the bottom at a rate j_B and the product at concentration C_P is removed from the top (i.e. in the foam) at a rate j_P. The surface flux j_S is calculated from j_P and r via j_S=3j_g/r.

The column of foam has an essentially constant liquid volume fraction ε which can be calculated by numerically solving the Stevenson and Li drainage equation (using m=0.016 and n=2) where ρ and μ are the liquid density and viscosity, and g is gravity:

`(μj_g)/(0.032ρgr²)=ε(1-ε)^2`

If ε>30% the "foam" calculations start to be meaningless so a warning red appears and the other calculated values can probably be ignored. The liquid flux in the foam j_P (this is the product removal rate because it is this flux which leaves the column) can then be calculated via:

`j_P=(εj_g)/(1-ε)-(ρgr^2mεn)/μ`

We can calculate the concentration in the bubble via the isotherm. If the concentration of the depleted liquid at the bottom of the column is C_B then the concentration in the product is given by:

`C_P=C_B+(Γ_mKC_B)/(1+KC_B).j_S/j_P`

Two more simple "balance" equations finish the job. Because j₀=j_P+j_B, i.e. the input flow is the same as the sum of the product flow and the bottom flow, and because we know the first two, j_B can be calculated. And j₀C₀=j_PC_P+j_BC_B, i.e. the total amount of the surface active agent going in is the same as that going out. By substituting C_P by the equation above we can solve the equation for the one remaining unknown, C_B. Well, not quite. We need two more values.

In a real process we want the maximum enrichment, E, combined with the maximum recovery, R and the maximum throughput j₀. As with any other similar process such as distillation or solvent extraction there is always a compromise. It is generally easy to get reasonable E and R values at low throughput. At reasonable throughputs there is a tradeoff between E and R and at high throughputs E is low. The new parameters are defined as:

`E=C_P/C_0`
`R=(j_PC_P)/(j_0C_0)`

A common trick in all such processes is to "reflux", to send some fraction χ of the product stream back into the system. This returned material needs to equilibrate with the stream of material rising through the common and it is common to define a number "theoretical plates" or "theoretical units" in the system which depend on many factors. It is too complex to describe the theory here (please refer to the book), but you can choose a value of χ and an NTU (Number of Theoretical Units) between 1 and 4. Of course if χ=0, with no reflux, then you get the values calculated via the above procedure. Indeed, these values are the starting point for the iterative solver and are provided as useful reference outputs. When χ is non-zero then j_P is replaced internally by j_T for the flow from the top of the foam column and we need j_R = χj_T for the reflux flow. Obviously our product flow is now given by j_P = (1-χ)j_T. Because the effect of χ is described by the graph, neither j_T nor j_R is provided as an output, but can readily be derived manually for any specific χ. At present it does not seem possible to know how many NTU one might have in a column so it is wise to assume at most 2, given that other assumptions such as perfect mixing and equilibration are unlikely to hold, making the idealised calculation over-optimistic. You can go up to 4 if you wish, but the numerics are more precarious.

My first implementation of the Stevenson and Li algorithm was numerically most inelegant and slow. I am most grateful to Dr Li for providing the code for a more elegant and faster algorithm. Responsibility for errors is mine.

Despite simplifications (e.g. that the bubbles are of a known single radius), reservations (e.g. about the number of NTU) and numerical glitches at some settings, this is still a very powerful tool for scientists and engineers to think through the tradeoffs that every production system faces. The absolute numbers are unlikely to be correct, but the trends will be correct and such an approach, in such a complex system, will almost always out-perform "intuition".

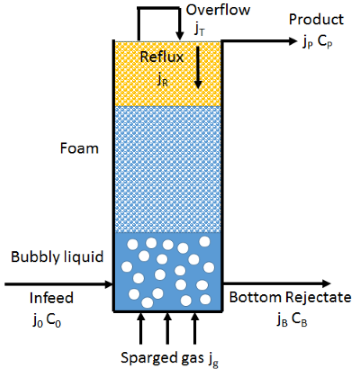An alternative to the external reflux is to do the same thing via an internal reflux where a portion of the foam is made to collapse towards the top of the column, achieving, in theory, exactly the same as external reflux with a simpler physical arrangement. The issue, of course, is that collapsing the bubbles in a controlled manner (e.g. by encouraging Ostwald ripening or coalescence) is hard to do, especially when playing with other settings at the same time. The diagram, therefore, is a highly stylised aspiration rather than a specific suggestion.