Latte Foams

One of my pleasures in life is to make a latte on my espresso machine. This gives two types of foam, the crema on the espresso and the foamed milk, with very different characteristics. The different sections of Practical Foams provide key insights into how to create the perfect latte. If you have reached here via a search engine and want a less science-heavy description then the CoffeeGeek.com site is ideal.

The espresso

Finely-ground freshly-roasted coffee beans, preferably Arabica, have hot water ~92°C pushed through them under high pressure (9 bar) for a relatively brief time (30s). This ensures a concentrated coffee with the maximum extraction of aroma chemicals and oils with the minimum of bitter acids (tannins) and an adequate amount of caffeine (slower extractions give higher caffeine kicks). It also creates a pleasing reddish-brown foam, the crema, which has aesthetic merits as well as the taste sensation provided by a foam full of aroma molecules which also acts to reduce the evaporative loss of aroma molecules between sips.

This summary of the complex science of a crema is based on the excellent review by Illy and Navarini¹. Clearly coffee doesn't contain large amounts of good foaming surfactants so getting a good crema is relatively hard, especially because, as we shall see, two key aspects of the foam actively fight against its stability. The surfactants are a complex mix of polysaccharides and browned protein complexes (containing melanoidins). The surface tension of the respective components are ~60 and ~46 mN/m - i.e. the polysaccharides are almost not surfactants but provide foam stability and the proteins are rather poor surfactants, though good enough to produce the modest amount of foam. This surfactant blend can be extracted with normal hot water, but the resulting coffee cannot then be induced to produce a good foam. The key to the crema is the 9bar pressure and a chemical that is produced in the coffee during roasting and which is (mostly) locked into the beans before grinding - CO2. During grinding plenty of CO2 is lost and right after grinding the rate of CO2 loss from the fine particles will be high - which is why espresso must use beans ground a moment before. Presumably one problem with grinding very fine (other than possible blocking of the espresso flow) is that CO2 loss during grinding will be much too high. During the extraction the CO2 is dissolved under the high pressure so that when the coffee emerges from the machine the bubbles instantly come out of solution, creating the foam. The downside of this process has been mentioned in the Ostwald section; CO2 has a high solubility in water and therefore diffuses rapidly through the foam walls so Ostwald ripening is fast. Anything in the system that introduced air rather than CO2 into the foam would create a foam more stable to ripening and therefore, as we know from the Drainage section, more stable to draining which is faster for larger bubbles. However, artificial attempts to induce air (cheap espresso machines) will tend to produce larger bubbles, giving a froth that will drain rapidly. One other message that emerges from the Ostwald modeller (and makes intuitive sense) is that the narrower the original distribution of bubble sizes, the less the ripening - with fewer bigger bubbles in the distribution there is less of a pressure gradient to power the diffusion process.

The second element which fights against a good crema is the oils and small (hydrophobic) particles in the coffee. It is well-known that Robusta coffees are easier to foam than Arabica - that's because the Arabica has ~3x more strongly hydrophobic oils and oils can be good antifoams. Because Arabica has more overall flavour, and because the o/w emulsion (created within the espresso process) adds to the richness of the overall drink, it is worth the extra effort required to get a good crema with the Arabica.

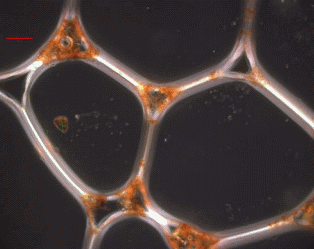As we know from the Antifoam section, if the oil drops or solid particles are very small they will tend to be swept out of the foam walls into the PB and nodes where they will act as "slow" antifoams only when signficant drainage has taken place. This effect is beautifully illustrated in the image taken from the Illy paper.

One classic way to make a fine emulsion is to force oil and water through a narrow orrifice under high pressure - a process not dissimilar to the espresso process. So again the high pressure will contribute to a good crema by minimising the size of the oil drops and making them less effective antifoams. Of course, high P_c values from tough protein/saccharide interfaces will also help resist the antifoam action. Over-roasting of coffee can reduce the saccharides and produce a less stable foam

From the Rheology section we know that smaller foam diameters lead to higher modulus and yield stress - i.e. a "firmer" foam. For espresso the "sugar test" is used to find out how long a known weight of sugar remains supported on the crema. It is a safe bet that the reason why higher pressures and fresher coffee will combine to give the firmest crema, is that they produce lots of small diameter bubbles.

What is the size of a good espresso bubble? This is important both for rheology and drainage as small is beautiful for both. From the Illy paper a representative Arabica espresso has bubbles in the 50µm range with a distribution which is either integral or has developed via Ostwald ripening from a smaller size. These small sizes are satisfyingly correct for good modulus/yield stress and low drainage. There is a lot of debate about the effects of free fatty acids within the coffee. To the extent that they form insoluble oil drops they might act as defoamers. To the extent that they migrate to the surface to create a solid wall (see previous discussions of "Gilette" foams) they can stabilise the foam against both ripening and drainage. Because the polysaccharides seem to dominate the stabilisation (low levels give low-stability foam) maybe the fatty acid effect is purely negative. With such a complex system it might be difficult to tell. But that's the delight of this scientific area: important scientific ideas are mingled with the pleasure of an exquisite cup of coffee.

The astonishing success of systems such as Nespresso or iperespresso is not due solely to marketing and convenience: the CO2 content in the Al-sealed capsules will be high, the grind packing denisty is, presumably, optimal and the controlled water temperature and controlled pressure build-up (governed by the capsule, not the tamped grounds) and sudden release might well be scientifically optimal for a good crema. Of crucial importance is that the capsule systems add a lot of air rather than CO2 and as mentioned above such foams will be slower to ripen. For a given coffee bean it is unlikely that such systems will produce a drink as good as that produced by a trained barista on an optimal machine. But the science suggests that it is likely to produce a better espresso than an average person on an average machine. To make my own position clear: I don't have a capsule machine nor do I want one; and, yes, I've had plenty of bad espressos from my low-quality machine but when things go well I'm very happy.

Milk foam

The latte needs a microfoam with a fascinating blend of properties:

• Wet (i.e. a high ε)
• Fine bubbles (small D)
• Stable for minutes at relatively high temperature
• Moderate viscosity (for a luxurious feel)
• Low yield stress (for easy pouring)

Arguably a cappuccino needs a dryer, coarser foam as it supposed to float on top of the coffee, and whilst there's nothing wrong with a cappuccino, this discussion is staying with my personal preference of a latte.

The surface tension of milk isn't far from that of water - so it is not full of free surfactants. Presumably the surfactants (mostly proteins) are wrapped around other parts of the milk so aren't available at the milk surface. To put it another way, it's rather hard to foam milk, and if you do foam it the result is a generally coarse foam that quickly falls apart for reasons we know well. The magic of the latte is the process that produces lots of small bubbles.

It is sometimes said that the bubbles are formed around steam. This has to be wrong - steam is water vapour and a steam bubble must collapse as soon as the water condenses. So a latte foam is an air foam. The steam is a source of heat (raising the milk temperature) but also of kinetic energy which drags the air into the milk. If the steam wand is placed too deep in the milk you end up with warm milk and no foam. The skilled barista with a simple wand or the amateur (like me) with a clever wand knows to place it just deep enough to entrain fine air into the milk, but not so shallow that a useless large froth is produced.

The main surfactant is, as with the crema, a protein which is (presumably) relatively slow to migrate to the interface (and maybe slow to be released from whatever is tying it up before foaming commences) and therefore a poor foamer, yet which produces a strong interface when it gets there so gives a stable foam. If the bubbles are small then drainage rates are smaller and the foam is relatively stiff (giving a luxurious feel) without being so stiff that pouring for latte art is impractical. If (at higher fats) you made a foam similar to that from whipping cream then the foam is strongly shear thinning but impossible to pour at low shear rates.

It is well-known that it is much easier to foam low-fat milk. We can guess why - the milk fat globules make a reasonable antifoam. At 4% fat in whole milk the foaming is hardest to achieve but the resulting drink is a proper latte - skimmed milk just isn't rich enough. At higher % fat the foaming becomes easier, but more like whipped cream where other effects take over - for example the o/w emulsion takes on a viscosity which can change drainage. The exact form of the fats present seems to make a big difference. Although whole milk is relatively standardised in overall composition, some types are poor foamers and "type" can mean different types of fresh milk or milks that change "type" over time. Presumably this is all down to subtle changes in the fat composition which can change the balance of oils from ineffective to effective antifoams; these changes can be in size and/or in hydrophobicity. It would take only a small change of balance between triglycerides and diglycerides to change the balance between antifoam and non-antifoam.

Everyone says that cold milk is required for the best foam. At least witn non-fat milk the optimum foaming temperature is around 40-60°C where "optimum" is a mixture of stability and (small) bubble diameter. So if one were foaming via some isothermal process, the perfect latte would use milk pre-heated to the optimum serving temperature around 60°C. Presumably because foam creation is rather slow and inefficient and because the foaming device (the steam) increases the temperature, you need to start cool to give time before the milk reaches ~65°C when the proteins start to denature and foaming ability is destroyed. You cannot re-foam milk that has been up to this temperature. At this higher temperature other changes take place to reduce the roundness of the milk taste (it tastes "scalded") so it is vital to stop at the right point. The reason for the optimum foaming temperature seems to be that the caseins (themselves useless foamers) undergo a transition which renders them less good as stabilisers of the foams created via the protein surfactants.

It is often noted that warmed milk tastes sweeter. It is sometimes said that this is because the lactose (which has ~ 1/3 the sweetness of sucrose) becomes more soluble at higher temperatures, but I see no reason why lactose is not fully dissolved anyway. Others argue that the ratio of isomers (α and β) changes but the timescale seems wrong and the difference in sweetness between isomers seems to be small. It may just be an effect similar to that of fructose which is perceived as being much less sweet at low temperatures. However, there is ambiguity about whether cooled warmed milk tastes sweeter than the original milk. If it does then some extra chemistry (such as splitting lactose into glucose+galactose) is taking place, though that sounds implausible for these low temperatures and short times. My own experiments show no difference in sweetness between milk left to rise to room temperature and milk that was foamed and left to cool to room temp, even though when warm the milk was definitely sweeter.